题目内容
(本小题满分14分)
已知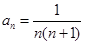 ,数列
,数列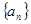 的前
的前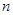 项的和记为
项的和记为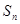 .
.
(1) 求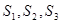 的值,猜想
的值,猜想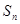 的表达式;
的表达式;
(2) 请用数学归纳法证明你的猜想.
已知
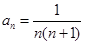 ,数列
,数列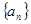 的前
的前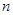 项的和记为
项的和记为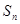 .
.(1) 求
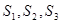 的值,猜想
的值,猜想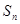 的表达式;
的表达式;(2) 请用数学归纳法证明你的猜想.
(1)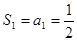 ,
,  ,
, 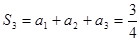
∴ 猜想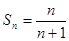 .
.
(2)证明:见解析。
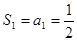 ,
,  ,
, 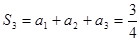
∴ 猜想
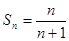 .
.(2)证明:见解析。
(1)因为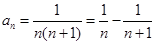 ,所以可分别求出a1,a2,a3,进而可求出S1,S2,S3.
,所以可分别求出a1,a2,a3,进而可求出S1,S2,S3.
(2)根据(1)可猜想出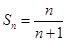 ,然后利用数学归纳法证明时要分两个步骤:
,然后利用数学归纳法证明时要分两个步骤:
一先验证:当n=1时,等式成立;
二先假设n=k时,等式成立;再证明当n=k+1时,等式也成立.在证明n=k+1时,一定要用上n=k时的归纳假设,否则证明无效.
(1)∵
∴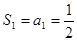 ,
,  ,
, 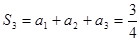
∴ 猜想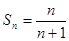 .
.
(2)证明:① 当 时,
时,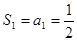 ,猜想成立
,猜想成立
② 假设当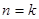 时,猜想成立,即:
时,猜想成立,即: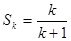 .
.
当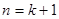 时,
时,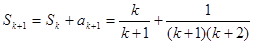
 .
.
∴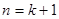 时猜想成立.
时猜想成立.
∴ 由 ①、②得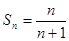 得证.
得证.
注:若没声明方法,也可用裂项求和法求得.
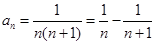 ,所以可分别求出a1,a2,a3,进而可求出S1,S2,S3.
,所以可分别求出a1,a2,a3,进而可求出S1,S2,S3.(2)根据(1)可猜想出
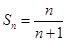 ,然后利用数学归纳法证明时要分两个步骤:
,然后利用数学归纳法证明时要分两个步骤:一先验证:当n=1时,等式成立;
二先假设n=k时,等式成立;再证明当n=k+1时,等式也成立.在证明n=k+1时,一定要用上n=k时的归纳假设,否则证明无效.
(1)∵

∴
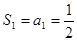 ,
,  ,
, 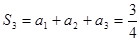
∴ 猜想
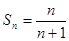 .
.(2)证明:① 当
 时,
时,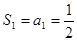 ,猜想成立
,猜想成立② 假设当
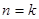 时,猜想成立,即:
时,猜想成立,即: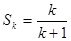 .
.当
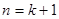 时,
时,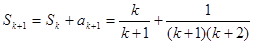
 .
.∴
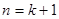 时猜想成立.
时猜想成立.∴ 由 ①、②得
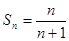 得证.
得证.注:若没声明方法,也可用裂项求和法求得.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
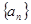 的各项都为正数,其前
的各项都为正数,其前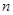 项和为
项和为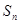 ,已知对任意
,已知对任意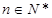 ,
,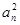 和
和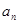 的等差中项.
的等差中项.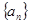 的通项公式;
的通项公式;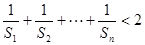 .
.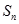 为数列
为数列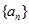 的前
的前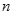 项和,对任意的
项和,对任意的 ,都有
,都有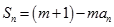
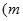 为常数,且
为常数,且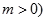 .
.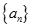 是等比数列;
是等比数列;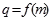 ,数列
,数列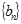 满足
满足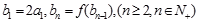 ,求数列
,求数列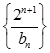 的前
的前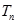 .
.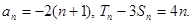
 ,求dn;
,求dn;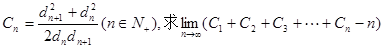 的值.
的值. 的前
的前 项和记为
项和记为 ,已知
,已知 .
. ;
; ,求数列
,求数列 的前
的前 .
.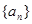 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第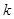 个1和第
个1和第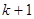 个1之间有
个1之间有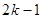 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前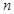 项的和为
项的和为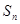 .
.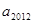 和
和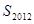 ;
;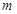 ,使得
,使得 ?如果存在,求出
?如果存在,求出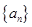 满足
满足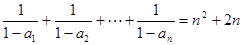
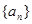 的通项公式;
的通项公式;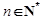 ,不等式
,不等式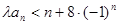 恒成立,求实数
恒成立,求实数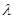 的取值范围.
的取值范围. ,等比中项是
,等比中项是 ,则曲线
,则曲线 的离心率为( )
的离心率为( ) B.
B. C.
C. D.
D. B.
B. C.
C. D.
D.
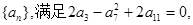 数列
数列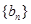 是等比数列,且
是等比数列,且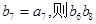 = ( )
= ( )