题目内容
已知数列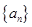 满足
满足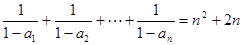
(1)求数列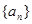 的通项公式;
的通项公式;
(2)若对任意的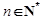 ,不等式
,不等式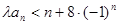 恒成立,求实数
恒成立,求实数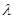 的取值范围.
的取值范围.
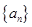 满足
满足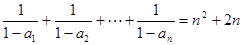
(1)求数列
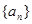 的通项公式;
的通项公式;(2)若对任意的
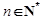 ,不等式
,不等式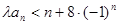 恒成立,求实数
恒成立,求实数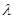 的取值范围.
的取值范围.(1) 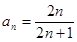 (2)
(2) 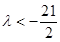
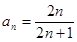 (2)
(2) 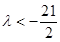
本试题组要是考查了数列的通项公式的七届和数列中前n项和的最值问题的综合运用。
(1)因为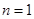 时有
时有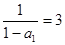 ,所以
,所以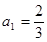
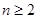 时,有
时,有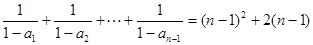
从而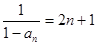 ,整体思想是解决的关键
,整体思想是解决的关键
(2)由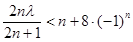 得
得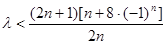 ,对于n分为奇数和偶数来得到证明。
,对于n分为奇数和偶数来得到证明。
解:(1)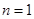 时有
时有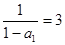 ,所以
,所以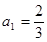
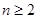 时,有
时,有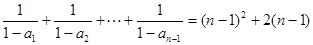
从而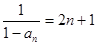 ,得
,得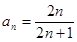 ,此式对
,此式对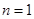 也适用
也适用
综上,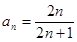 ……………6分
……………6分
(2)由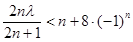 得
得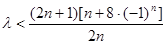
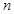 为奇数时,
为奇数时,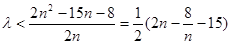
当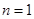 时,
时, 取得最小值
取得最小值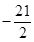 ,所以此时有
,所以此时有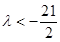
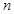 为偶数时,
为偶数时,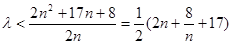
当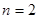 时,
时,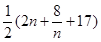 取得最小值
取得最小值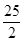 ,所以此时有
,所以此时有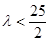
综上,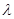 的取值范围是
的取值范围是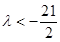 ……………………….12分
……………………….12分
(1)因为
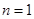 时有
时有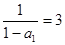 ,所以
,所以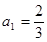
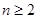 时,有
时,有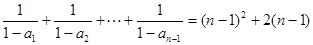
从而
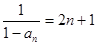 ,整体思想是解决的关键
,整体思想是解决的关键(2)由
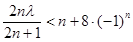 得
得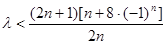 ,对于n分为奇数和偶数来得到证明。
,对于n分为奇数和偶数来得到证明。解:(1)
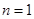 时有
时有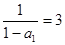 ,所以
,所以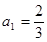
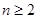 时,有
时,有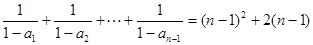
从而
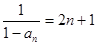 ,得
,得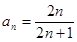 ,此式对
,此式对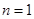 也适用
也适用综上,
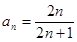 ……………6分
……………6分(2)由
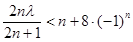 得
得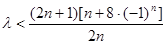
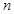 为奇数时,
为奇数时,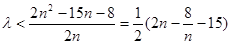
当
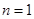 时,
时, 取得最小值
取得最小值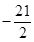 ,所以此时有
,所以此时有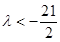
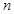 为偶数时,
为偶数时,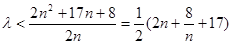
当
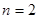 时,
时,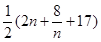 取得最小值
取得最小值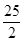 ,所以此时有
,所以此时有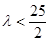
综上,
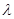 的取值范围是
的取值范围是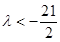 ……………………….12分
……………………….12分
练习册系列答案
相关题目
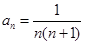 ,数列
,数列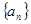 的前
的前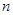 项的和记为
项的和记为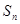 .
.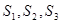 的值,猜想
的值,猜想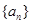 满足
满足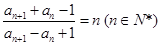 ,且
,且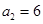 。
。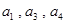 。
。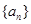 的前
的前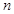 项和
项和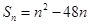
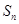 的最大或最小值
的最大或最小值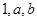 ,等比数列
,等比数列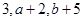 ,那么等差数列的公差为( )
,那么等差数列的公差为( )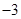
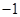
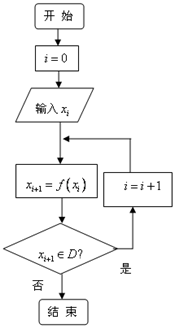
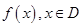 ,可按右图构造一个数列发生器.记由数列发生器产生数列
,可按右图构造一个数列发生器.记由数列发生器产生数列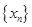 .
.
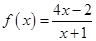 ,且输入
,且输入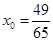 ,请写出数列
,请写出数列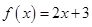 ,且输入
,且输入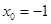 ,求数列
,求数列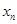 .
.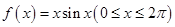 ,且要产生一个无穷的常数列
,且要产生一个无穷的常数列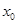 的值及相应数列
的值及相应数列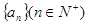 是等差数列,
是等差数列,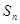 是其前
是其前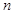 项和,
项和,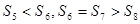 ,则下列结论错误的是( )
,则下列结论错误的是( )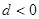
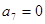
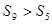
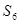 与
与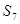 均为
均为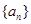 是首项为2,公差为1的等差数列,
是首项为2,公差为1的等差数列,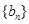 是首项为1,公比为2的等比数列,则数列
是首项为1,公比为2的等比数列,则数列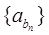 前10项的和等于 ( )
前10项的和等于 ( )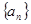 中,若
中,若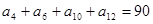 ,则
,则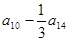 =
=