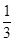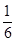题目内容
设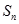 为数列
为数列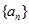 的前
的前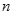 项和,对任意的
项和,对任意的 ,都有
,都有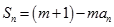
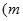 为常数,且
为常数,且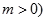 .
.
(1)求证:数列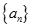 是等比数列;
是等比数列;
(2)设数列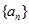 的公比
的公比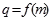 ,数列
,数列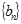 满足
满足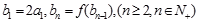 ,求数列
,求数列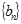 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列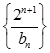 的前
的前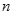 项和
项和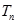 .
.
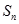 为数列
为数列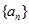 的前
的前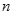 项和,对任意的
项和,对任意的 ,都有
,都有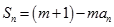
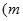 为常数,且
为常数,且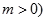 .
.(1)求证:数列
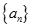 是等比数列;
是等比数列;(2)设数列
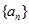 的公比
的公比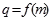 ,数列
,数列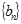 满足
满足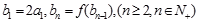 ,求数列
,求数列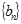 的通项公式;
的通项公式;(3)在满足(2)的条件下,求数列
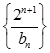 的前
的前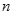 项和
项和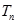 .
.(1)证明:当 时,
时,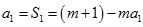 ,解得
,解得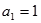 .…………………1分
.…………………1分
当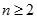 时,
时, .即
.即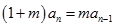 .………2分
.………2分
又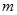 为常数,且
为常数,且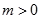 ,∴
,∴
 . ………………………3分
. ………………………3分
∴数列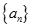 是首项为1,公比为
是首项为1,公比为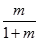 的等比数列. ……………………4分
的等比数列. ……………………4分
(2)解:由(1)得,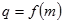
 ,
, . ………………………5分
. ………………………5分
∵ ,∴
,∴ ,即
,即
 .………7分
.………7分
∴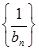 是首项为
是首项为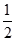 ,公差为1的等差数列.………………………………………8分
,公差为1的等差数列.………………………………………8分
∴ ,即
,即 (
( ).………………………9分
).………………………9分
(3)解:由(2)知 ,则
,则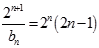 .
.
所以 , ………………10分
, ………………10分
即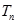
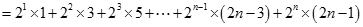 , ① ……11分
, ① ……11分
则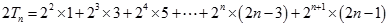 , ②………12分
, ②………12分
②-①得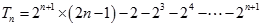 , ……………………13分
, ……………………13分
故 . ………………14分
. ………………14分
 时,
时,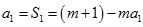 ,解得
,解得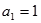 .…………………1分
.…………………1分当
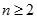 时,
时, .即
.即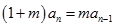 .………2分
.………2分又
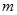 为常数,且
为常数,且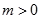 ,∴
,∴
 . ………………………3分
. ………………………3分∴数列
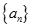 是首项为1,公比为
是首项为1,公比为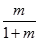 的等比数列. ……………………4分
的等比数列. ……………………4分(2)解:由(1)得,
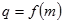
 ,
, . ………………………5分
. ………………………5分∵
 ,∴
,∴ ,即
,即
 .………7分
.………7分∴
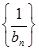 是首项为
是首项为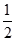 ,公差为1的等差数列.………………………………………8分
,公差为1的等差数列.………………………………………8分∴
 ,即
,即 (
( ).………………………9分
).………………………9分(3)解:由(2)知
 ,则
,则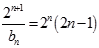 .
.所以
 , ………………10分
, ………………10分即
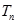
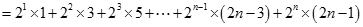 , ① ……11分
, ① ……11分则
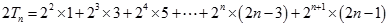 , ②………12分
, ②………12分②-①得
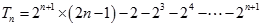 , ……………………13分
, ……………………13分故
 . ………………14分
. ………………14分本题主要考查等比数列的性质.当出现等比数列和等差数列相乘的形式时,求和可用错位相减法.
(1)当n≥2时,根据an=Sn-Sn-1,进而得出an和an-1的关系整理得an an-1 =m
an-1 =m ( 1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.
( 1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.
(2)根据(1)可得f(m)的解析式.再根据bn=f(bn-1)整理可得(1 bn) -(1
bn) -(1 bn-1) =1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.
bn-1) =1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.
(3)把(2)中的bn代入{2n+1 bn },再通过错位相减法求得Tn
bn },再通过错位相减法求得Tn
(1)当n≥2时,根据an=Sn-Sn-1,进而得出an和an-1的关系整理得an
 an-1 =m
an-1 =m ( 1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.
( 1+m) ,因m为常数,进而可证明当n≥2时数列{an}是等比数列.,当n=1时等式也成立,原式得证.(2)根据(1)可得f(m)的解析式.再根据bn=f(bn-1)整理可得(1
 bn) -(1
bn) -(1 bn-1) =1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.
bn-1) =1进而推知数列{bn}为等差数列,首项为2a1,公差为1,再根据等差数列的通项公式可得答案.(3)把(2)中的bn代入{2n+1
 bn },再通过错位相减法求得Tn
bn },再通过错位相减法求得Tn
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
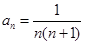 ,数列
,数列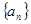 的前
的前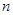 项的和记为
项的和记为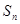 .
.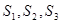 的值,猜想
的值,猜想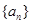 满足
满足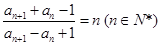 ,且
,且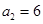 。
。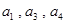 。
。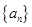 满足:
满足: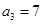 ,
,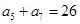 ,
,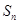 .
.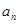 及前n项和
及前n项和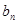 =
=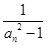 (n
(n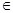 N*),求数列
N*),求数列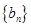 的前n项和
的前n项和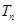 .
.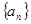 为等差数列,
为等差数列,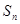 是等差数列的前
是等差数列的前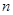 项和,已知
项和,已知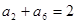 ,
,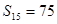 .
.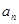 ;
;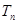 为数列
为数列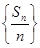 的前
的前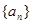 的前
的前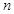 项和为
项和为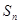 ,如果存在正整数
,如果存在正整数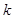 和
和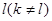 ,使得
,使得 ,
, ,则( )
,则( )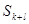 的最小值为
的最小值为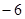
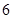
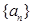 的前
的前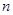 项和为
项和为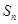 ,点
,点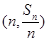 在直线
在直线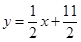 上.数列
上.数列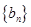 满足
满足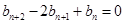
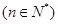 ,
,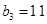 ,且其前9项和为153.
,且其前9项和为153.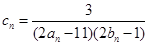 ,数列
,数列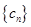 的前
的前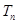 ,求使不等式
,求使不等式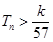 对一切
对一切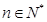 都成立的最大正整数
都成立的最大正整数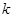 的值.
的值.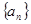 中,
中,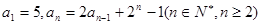 ,若存在实数
,若存在实数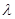 ,使得数列
,使得数列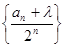 为等差数列,则
为等差数列,则 是等差数列
是等差数列 的前n项和,
的前n项和, ,则
,则 的值为 ( ).
的值为 ( ).