题目内容
若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意正整数n,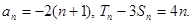
(1)求数列{bn}的通项公式;
(2)在平面直角坐标系内,直线ln的斜率为bn,且与抛物线y = x2有且仅有一个交点,与y轴交
于点Dn,记 ,求dn;
,求dn;
(3)若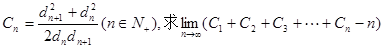 的值.
的值.
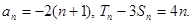
(1)求数列{bn}的通项公式;
(2)在平面直角坐标系内,直线ln的斜率为bn,且与抛物线y = x2有且仅有一个交点,与y轴交
于点Dn,记
 ,求dn;
,求dn;(3)若
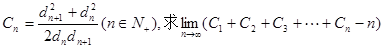 的值.
的值.(1)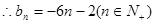
(2)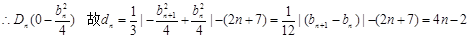
(3)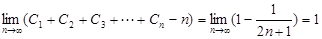 。
。
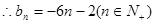
(2)
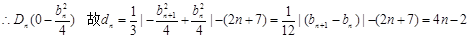
(3)
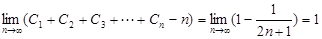 。
。本试题主要是考查的直线与抛物线的位置关系,以及数列的求和,和数列通项公式的运用。
(1)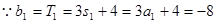
当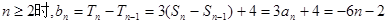
n = 1时也适合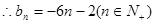
(2)设出直线方程与抛物线联立方程组得到设ln方程为: 由
由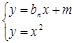 有:
有: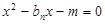 ∵直线ln与抛物有且只有一个交点,
∵直线ln与抛物有且只有一个交点, 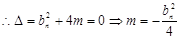
(3)因为 ,裂项求和得到结论。
,裂项求和得到结论。
(1)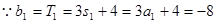
当
n = 1时也适合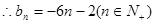
(2)设ln方程为: 由
由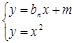 有:
有: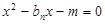
∵直线ln与抛物有且只有一个交点,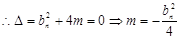
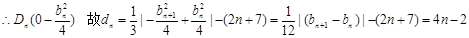
(3)

故
(1)
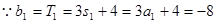
当
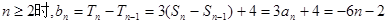
n = 1时也适合
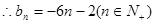
(2)设出直线方程与抛物线联立方程组得到设ln方程为:
 由
由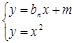 有:
有: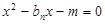 ∵直线ln与抛物有且只有一个交点,
∵直线ln与抛物有且只有一个交点, 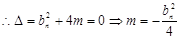
(3)因为
 ,裂项求和得到结论。
,裂项求和得到结论。(1)
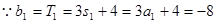
当

n = 1时也适合
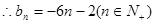
(2)设ln方程为:
 由
由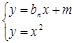 有:
有: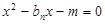
∵直线ln与抛物有且只有一个交点,
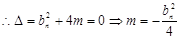
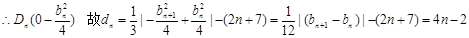
(3)


故


练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
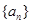 中,
中,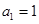 ,且点
,且点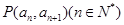 在直线
在直线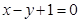 上.
上. 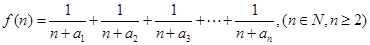 ,求证
,求证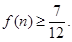
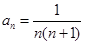 ,数列
,数列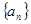 的前
的前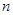 项的和记为
项的和记为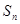 .
.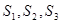 的值,猜想
的值,猜想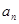 ﹜满足:
﹜满足: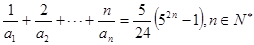 .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛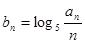 ,求
,求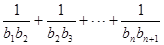
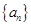 满足:
满足: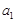 =
=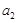 =2,
=2,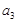 =3,
=3,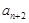 =
=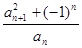 (
(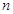 ≥2)
≥2)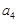 ,
,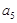 ,
,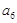 ;
;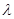 ,使得数列
,使得数列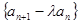 (
(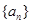 的前n项和为
的前n项和为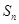 ,点
,点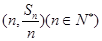 均在函数y=3x-2的图像上。
均在函数y=3x-2的图像上。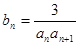 ,
,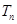 是数列
是数列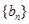 的前n项和,求使得
的前n项和,求使得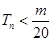 对所有
对所有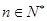 都成立的最小正整数m。
都成立的最小正整数m。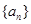 的前
的前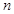 项和
项和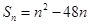
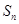 的最大或最小值
的最大或最小值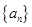 满足:
满足: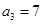 ,
,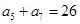 ,
,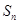 .
.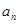 及前n项和
及前n项和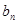 =
=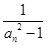 (n
(n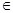 N*),求数列
N*),求数列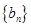 的前n项和
的前n项和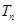 .
.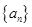 是公差不为零的等差数列,它的前
是公差不为零的等差数列,它的前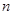 项和为
项和为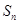 ,且
,且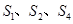 成等比数列,则
成等比数列,则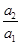 等于 ( )
等于 ( )