题目内容
【题目】如图，已知椭圆C： 
（a>b>0）的离心率为
，F为椭圆C的右焦点.A（-a，0），|AF|=3.
（I）求椭圆C的方程；
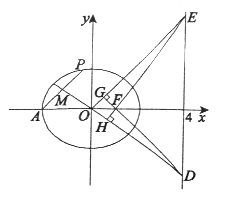
（II）设O为原点，P为椭圆上一点，AP的中点为M.直线OM与直线x=4交于点D，过O且平行于AP的直线与直线x=4交于点E.求证：∠ODF=∠OEF.
【答案】.（I）
；（II）证明见解析.
【解析】试题分析：（1）根据椭圆的离心率为
， 
，结合性质
，列出关于
、
、
的方程组，求出
、
、
，即可得椭圆C的方程；（2）设直线
的方程为： 
，将其代入椭圆方程，整理得
，根据韦达定理可得
（
， 
），直线
的方程是
，令
，得
，同理可得
，根据斜率公式可得在
和
中， 
和
都与
互余，所以
.
试题解析：（I）设椭圆C的半焦距为c.依题意，得
，a+c=3. 解得a=2，c=1.
所以b2=a2-c2=3，所以椭圆C的方程是
（II）由（I）得A（-2，0）.设AP的中点M（x0，y0），P（x1，y1）.
设直线AP的方程为：y=k（x+2）（k≠0），将其代入椭圆方程，整理得
（4k2+3）x2+16k2x+16k2-12=0，
所以-2+x1=
.
所以x0=
，y0=k（x0+2）=
，
即M（
， 
）.
所以直线OM的斜率是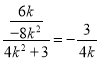
，
所以直线OM的方程是y=-
x.令x=4，得D（4，-
）.
直线OE的方程是y=kx.令x=4，得E（4，4k）.
由F（1，0），得直线EF的斜率是
=
，所以EF⊥OM，记垂足为H；
因为直线DF的斜率是
=
，所以DF⊥OE，记垂足为G.
在Rt△EHO和Rt△DGO中，∠ODF和∠OEF都与∠EOD互余，
所以∠ODF=∠OEF.
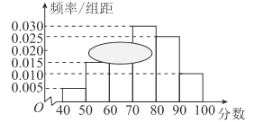
名校课堂系列答案
【题目】目前我国城市的空气污染越来越严重，空气质量指数
一直居高不下，对人体的呼吸系统造成了严重的影响，现调查了某城市500名居民的工作场所和呼吸系统健康，得到
列联表如下：
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
（Ⅰ）请把列联表补充完整；
（Ⅱ）你是否有95%的把握认为感染呼吸系统疾病与工作场所有关；
（Ⅲ）现采用分层抽样从室内工作的居民中抽取一个容量为6的样本，将该样本看成一个总体，从中随机抽取2人，求2人都有呼吸系统疾病的概率.
参考公式与临界表：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
