题目内容
5.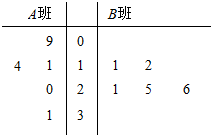 长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
分析 (Ⅰ)求出A,B班样本数据的平均值,估计A,B两班的学生平均每周上网时长的平均值;
(Ⅱ)先计算从A班和B班的样本数据中各随机抽取一个的情况总数,再计算a>b的情况种数,代入古典概型概率计算公式,可得答案.
解答 解:(Ⅰ)A班样本数据的平均值为$\frac{1}{5}$(9+11+14+20+31)=17,
由此估计A班学生每周平均上网时间17小时;
B班样本数据的平均值为$\frac{1}{5}$(11+12+21+25+26)=19,
由此估计B班学生每周平均上网时间较长.
(Ⅱ)A班的样本数据中不超过21的数据有3个,分别为:9,11,14,
B班的样本数据中不超过21的数据也有3个,分别为:11,12,21,
从A班和B班的样本数据中各随机抽取一个共有:9种不同情况,
分别为:(9,11),(9,12),(9,21),(11,11),(11,12),(11,21),(14,11),(14,12),(14,21),
其中a>b的情况有(14,11),(14,12)两种,
故a>b的概率P=$\frac{2}{9}$
点评 本题考查的知识点是古典概型概率计算公式,茎叶图的应用,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知点(x,y)在如图所示的阴影部分内(含边界)运动,则z=x+2y的最大值是( )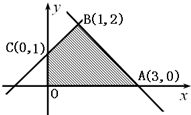

| A. | 0 | B. | 2 | C. | 3 | D. | 5 |
14.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |