题目内容
4．为了缓解城市拥堵，某市对非居民区的公共停车场制定了不同的收费标准（见表）．| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
| A． | 一类 | B． | 二类 | C． | 三类 | D． | 无法判断 |
分析 根据已知中三类地区公共停车场制定了不同的收费标准，结合已知小王某次停车3小时，缴费24元，可得答案．
解答 解：如果停车在一类区域，则停车3小时，缴费2.5×4+3.75×8=40元；
如果停车在二类区域，则停车3小时，缴费1.5×4+2.25×8=24元；
如果停车在三类区域，则停车3小时，缴费0.5×4+0.75×8=8元；
故小王该次停车所在地区的类别是二类，
故选：B
点评 本题考查的知识点是分段函数的简单应用，难度不大，属于基础题．
练习册系列答案
相关题目
14．从左至右依次站着甲、乙、丙3个人，从中随机抽取2个人进行位置调换，则经过两次这样的调换后，甲在乙左边的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{4}{9}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右支上的一点P（x0，y0）到左焦点的距离与到右焦点的距离之差为2$\sqrt{2}$，且到两条渐进线的距离之积为$\frac{2}{3}$，则该双曲线的离心率为（ ）
| A． | $\sqrt{5}$ | B． | $\sqrt{6}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{6}}{2}$ |
9．已知向量$\overrightarrow{a}$=（x，1），$\overrightarrow{b}$=（4，x），$\overrightarrow{a}$∥$\overrightarrow{b}$，则实数x的值是（ ）
| A． | 0 | B． | ±2 | C． | 2 | D． | -2 |
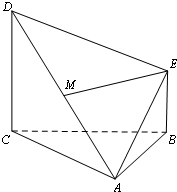如图，多面体ABCDE中，CD⊥平面ABC，BE⊥平面ABC，AB=BC，BE=$\frac{1}{2}$CD，