题目内容
2.设F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,O为坐标原点,点A,B分别在双曲线的两条渐近线上,AF⊥x轴,BF∥OA,$\overrightarrow{AB}$•$\overrightarrow{OB}$=0,则该双曲线的离心率为$\frac{2\sqrt{3}}{3}$.分析 设kOB=-$\frac{b}{a}$,利用$\overrightarrow{AB}$•$\overrightarrow{OB}$=0,可得kAB=$\frac{a}{b}$,再求出A,B的坐标,可得kAB=$\frac{3b}{a}$,即可求出双曲线的离心率.
解答 解:由题意,设kOB=-$\frac{b}{a}$,
∵$\overrightarrow{AB}$•$\overrightarrow{OB}$=0,
∴kAB=$\frac{a}{b}$,
直线FB的方程为y=$\frac{b}{a}$(x-c),
与y=-$\frac{b}{a}$x联立可得B($\frac{c}{2}$,-$\frac{bc}{2a}$)
∵A(c,$\frac{bc}{a}$),
∴kAB=$\frac{3b}{a}$=$\frac{a}{b}$,
∴b2=$\frac{1}{3}$a2,
∴c2=a2+b2=$\frac{4}{3}$a2,
∴e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的离心率,考查向量知识,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
10.已知点(x,y)在如图所示的阴影部分内(含边界)运动,则z=x+2y的最大值是( )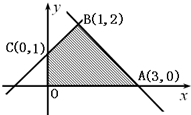

| A. | 0 | B. | 2 | C. | 3 | D. | 5 |
14.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
11.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递减函数是( )
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=x3 | C. | f(x)=($\frac{1}{2}$)x | D. | f(x)=3x |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上的一点P(x0,y0)到左焦点的距离与到右焦点的距离之差为2$\sqrt{2}$,且到两条渐进线的距离之积为$\frac{2}{3}$,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |