题目内容
18.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,斜率k(k≥0)的直线l过椭圆中心O且与椭圆的两个交点从左至右为E,G,与直线l垂直的直线m与椭圆的两个交点,从上至下为F,H,当四边形EFGH为正方形时面积为$\frac{8}{3}$.(1)求椭圆的方程;
(2)求四边形EFGH的面积S的取值范围.
分析 (1)当四边形EFGH为正方形时面积为$\frac{8}{3}$,G的坐标为($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),代入椭圆方程,结合椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,求出a,b,即可求椭圆的方程;
(2)分类讨论,求出面积,利用基本不等式求四边形EFGH的面积S的取值范围.
解答 解:(1)当四边形EFGH为正方形时面积为$\frac{8}{3}$,G的坐标为($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),
代入椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{2}{3{a}^{2}}+\frac{2}{3{b}^{2}}=1$,
∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,
∴$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
∴a=$\sqrt{2}b$,
∴b=1,a=$\sqrt{2}$,
∴椭圆的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)k≠0,设直线EG的方程为y=kx,代入椭圆方程,可得G($\sqrt{\frac{2}{1+2{k}^{2}}}$,$\sqrt{\frac{2}{1+2{k}^{2}}}$),
同理F(-$\sqrt{\frac{2{k}^{2}}{{k}^{2}+2}}$,$\sqrt{\frac{2{k}^{2}}{{k}^{2}+2}}$),
∴四边形EFGH的面积S=4×$\frac{1}{2}$×$\sqrt{\frac{2}{1+2{k}^{2}}}$×$\sqrt{\frac{2{k}^{2}}{{k}^{2}+2}}$=$\sqrt{\frac{{k}^{2}}{(1+2{k}^{2})({k}^{2}+2)}}$=$\sqrt{2{k}^{2}+\frac{2}{{k}^{2}}+5}$≥$\sqrt{5+4}$=3,
k=0时,S=4×$\frac{1}{2}×\sqrt{2}×1$=2$\sqrt{2}$.
∴四边形EFGH的面积S的取值范围是[3,+∞).
点评 本题考查椭圆方程,考查直线与 椭圆的位置关系,考查面积的计算,考查学生分析解决问题的能力,属于中档题.

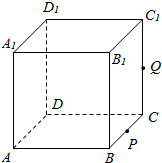 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则当CQ∈(0,$\frac{1}{2}$]∪{1}.时,S为四边形;当CQ=$\frac{1}{2}$时S为等腰梯形;当CQ=1时,S的面积为$\frac{\sqrt{6}}{2}$. 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论: