��Ŀ����
9��������ֱ��l������C1������C2�����У��������C1������C2Ϊ��������ߡ����������ĸ����⣺������ֻ������ֱ��lʹ������C1��x2+y2=4������C2��x2+y2-4x+2y+4=0Ϊ��������ߡ���
������C1��y=$\frac{1}{2}\sqrt{{x^2}+1}$������C2��y=$\frac{1}{2}\sqrt{{x^2}-1}$�ǡ�������ߡ���
�۵�b��a��0ʱ������C1��y2=4ax������C2����x-b��2+y2=a2һ�����ǡ�������ߡ���
�ܱش�������aʹ������C1��y=alnx������C2��y=x2-xΪ��������ߡ���
������ȷ����ĸ���Ϊ��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �٣��������߶���Բ��ֻ���о���Բ��λ�ù�ϵ���ɣ�
�������жϣ����������ǹ���˫���ߣ���x���Ϸ��IJ��֣�����֪û�й����ߣ�
����֪Բ�������ߵġ��ڲ��������Բ����ܴ��ڹ����ߣ�
�������õ������C1�����ߣ�Ȼ���������C2�������б�ʽ��������⣮
��� �⣺����֪��C1�����ԣ�0��0��ΪԲ�ģ�r=2��Բ��C2�����ԣ�2��-1��ΪԲ�ģ�r=1��Բ��Բ�ľ�=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$�����ڰ뾶֮��1��С�ڰ뾶֮��3������Բ�ཻ���������������ߣ��ʢ���ȷ��
����֪������C1��C2�ǹ���˫���ߣ����Ǹ�����x���Ϸ��IJ��֣������������û�й����ߣ��ʢڴ���
����Ϊb��a��0��������ͬһ����ϵ���������ǵ�ͼ�����£�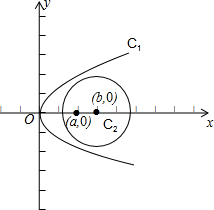
���������߲����й����ߣ��ʢ���ȷ��
�ܵ�a=1ʱ��C1��y=lnx�������x=1ʱ�����߷���Ϊy=x-1������C2����x=1ʱ�����߷���2Ϊy=x-1���ʢ���ȷ��
����������������ȷ��
��ѡ��C��
���� ���⿼����Բ���ߵı����̼������ʡ����߷��̵���ͬʱ����Ϊ�¶������⣬Ҫע��ԡ���������⣮

��ϰ��ϵ�д�
 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
19����֪�գ�x��=x��x-m��2��x=1��ȡ�ü�Сֵ���Һ���f��x����g��x������f��5��=2��f�䣨5��=3m��g��5��=4��g�䣨5��=m������F��x��=$\frac{f��x��+2}{g��x��}$��ͼ����x=5�������߷���Ϊ��������
| A�� | 3x-2y-13=0 | B�� | 3x-2y-13=0��x-2y-3=0 | ||
| C�� | x-2y-3=0 | D�� | x-2y-3=0��2x+3y-13=0 |
17����֪����={��x��y��|$\left\{\begin{array}{l}{-1��x��1}\\{-1��y��1}\end{array}\right.$������A={��x��y��|0��y��$\frac{1}{2}$e-|x|��x��[-1��1]���ڦ������Ͷ��һ��M�����M��������A�ڵĸ����ǣ�������
| A�� | $\frac{1}{2}$��1-$\frac{1}{e}$�� | B�� | $\frac{1}{4}$��1-$\frac{1}{e}$�� | C�� | $\frac{1}{e}$ | D�� | 1-$\frac{1}{e}$ |
4��${��}_{0}^{1}$��$\sqrt{1-{x}^{2}}$-x��dx���ڣ�������
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{��-1}{4}$ | D�� | $\frac{��-2}{4}$ |
1������y=cos2x-2cosx+1����Сֵ�����ֵ�ֱ��ǣ�������
| A�� | -$\frac{1}{2}$��4 | B�� | 0��4 | C�� | -$\frac{1}{4}$��2 | D�� | 0��2 |
 ��ͼĦ���ְ뾶10�ף���͵�A�����0.5�ף���֪Ħ���ְ���ʱ�뷽��ÿ3����תһȦ�����ʾ��ȣ����˴���͵�A��ȥ�ҿ�ʼ��ʱ����t�ַ��Ӻ������10sin��$\frac{2}{3}��$t$-\frac{��}{2}$��+10.5��10.5-10cos��$\frac{2}{3}$��t���ף�
��ͼĦ���ְ뾶10�ף���͵�A�����0.5�ף���֪Ħ���ְ���ʱ�뷽��ÿ3����תһȦ�����ʾ��ȣ����˴���͵�A��ȥ�ҿ�ʼ��ʱ����t�ַ��Ӻ������10sin��$\frac{2}{3}��$t$-\frac{��}{2}$��+10.5��10.5-10cos��$\frac{2}{3}$��t���ף�