题目内容
17.已知区域Ω={(x,y)|$\left\{\begin{array}{l}{-1≤x≤1}\\{-1≤y≤1}\end{array}\right.$,区域A={(x,y)|0≤y≤$\frac{1}{2}$e-|x|,x∈[-1,1],在Ω内随机投掷一点M,则点M落在区域A内的概率是( )| A. | $\frac{1}{2}$(1-$\frac{1}{e}$) | B. | $\frac{1}{4}$(1-$\frac{1}{e}$) | C. | $\frac{1}{e}$ | D. | 1-$\frac{1}{e}$ |
分析 本题符合几何概型,所以只要分别求出两个区域的面积,利用面积比求概率.
解答 解:由题意,两个区域对应的图形如下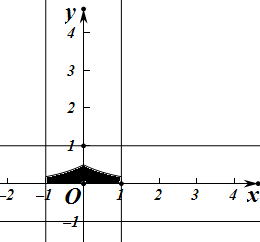 ,区域Ω是图中边长为2的正方形,区域A是阴影部分,面积为${2∫}_{0}^{1}\frac{1}{2}{e}^{-x}dx$=2($-\frac{1}{2}{e}^{-x}$)${\;}_{0}^{1}$=1-$\frac{1}{e}$,
,区域Ω是图中边长为2的正方形,区域A是阴影部分,面积为${2∫}_{0}^{1}\frac{1}{2}{e}^{-x}dx$=2($-\frac{1}{2}{e}^{-x}$)${\;}_{0}^{1}$=1-$\frac{1}{e}$,
由几何概型公式可得点M落在区域A内的概率是$\frac{1-\frac{1}{e}}{2×2}=\frac{1}{4}(1-\frac{1}{e})$;
故选B.
点评 本题考查了利用定积分求曲边梯形的面积以及几何概型公式的运用;关键是求出区域A的面积,利用几何概型公式解答.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
8.已知函数f(x)定义域为(0,+∞),且满足f(x)+xf′(x)=$\frac{lnx}{x}$,f(e)=$\frac{1}{e}$则下列结论正确的是( )
| A. | f(x)有极大值无极小值 | B. | f(x)有极小值无极大值 | ||
| C. | f(x)既有极大值又有极小值 | D. | f(x)没有极值 |
5.2015年3月份全国两会召开后,中国足球引起重视,某校对学生是否喜欢足球进行了抽样调查,男女生各抽了50名,相关数据如下表所示:
(1)用分层抽样的方法在喜欢足球的学生中随机抽取6名,男生应该抽取几名?
(2)在上述抽取的6名学生中任取2名,求恰有1名女生的概率.
(3)能否在犯错误的概率不超过0.005的前提下认为性别与喜欢足球有关系?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
| 不喜欢足球 | 喜欢足球 | 总计 | |
| 男生 | 18 | 32 | 50 |
| 女生 | 34 | 16 | 50 |
| 总计 | 52 | 48 | 100 |
(2)在上述抽取的6名学生中任取2名,求恰有1名女生的概率.
(3)能否在犯错误的概率不超过0.005的前提下认为性别与喜欢足球有关系?
参考公式及数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
| P(K≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10.828 |
2.已知实数x、y满足$\left\{\begin{array}{l}{y≤3}\\{3x-y-3≤0}\\{2x+y-2≥0}\end{array}\right.$,则目标函数z=2x-y的最大值为( )
| A. | -4 | B. | 1 | C. | 2 | D. | 3 |
2. 已知函数f(x)的导函数f′(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )
已知函数f(x)的导函数f′(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )
 已知函数f(x)的导函数f′(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )
已知函数f(x)的导函数f′(x)的图象如图所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),则不等式g(x)≥3x-3的解集是( )| A. | [-1,1]∪[2,+∞) | B. | (-∞,-1]∪[1,2] | C. | (-∞,-1]∪[2,+∞) | D. | [-1,2] |
 如图,AB是⊙O的直径,CB与⊙O相切于点B,E为线段BC上一点,连接AC,连接AE,分别交⊙O于D,G两点,连接DG交CB于点F.
如图,AB是⊙O的直径,CB与⊙O相切于点B,E为线段BC上一点,连接AC,连接AE,分别交⊙O于D,G两点,连接DG交CB于点F.