题目内容
12.已知关于x不等式|2x+a|>|x-1|在区间[2,3]上恒成立,则实数a的取值范围为a<-8或a>-3.分析 先去掉x-1的绝对值,再通过讨论2x+a的符号,得到关于a的不等式,从而求出a的范围.
解答 解:∵x∈[2,3],
∴x-1>0,
问题转化为不等式|2x+a|>x-1在区间[2,3]上恒成立,
①2x+a>0时,2x+a>x-1在区间[2,3]恒成立,
即a>-x-1在区间[2,3]恒成立,
∴a>(-x-1)max=-3,
②2x+a<0时,2x+a<-x+1在区间[2,3]恒成立,
即a<-3x+1在区间[2,3]恒成立,
∴a<(-3x+1)min=-8,
故答案为:a<-8或a>-3.
点评 本题考查了函数恒成立问题,考查解不等式问题,本题属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3.若某公司从四位大学毕业生甲、乙、丙、丁中录用两人,这四人被录用的机会均等,则甲被录用的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.如图是计算1+2+4+…+219的值的一个程序框图,则其中空白判断框内应填入的是( )
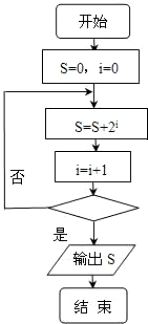

| A. | i=19 | B. | i≥20 | C. | i≤19 | D. | i≤20 |
17.函数f(x)=2x-sinx在(-∞,+∞)上( )
| A. | 是增函数 | B. | 是减函数 | C. | 有最大值 | D. | 有最小值 |
4.在研究高血压与患心脏病的关系调查中,调查了有高血压者30人,其中有20人患心脏病;调查的80个不高血压者中有30人患心脏病,
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
 B、
B、 C、
C、 D、
D、