题目内容
15．解关于a的方程：$\frac{-3}{a}$+$\frac{4}{12-a}$=1．分析 方程：$\frac{-3}{a}$+$\frac{4}{12-a}$=1．两边同乘以a（12-a），一元二次方程，并且经过检验即可得出．
解答 解：方程：$\frac{-3}{a}$+$\frac{4}{12-a}$=1．
两边同乘以a（12-a），化为-3（12-a）+4a=a（12-a），
化为a2-5a-36=0，
因式分解为（a-9）（a+4）=0，
解得：x=9，或a=-4．
经过检验都满足方程．
∴方程的解为：x=9，或a=-4．
点评 本题考查了分式方程与一元二次方程的解法，考查了计算能力，属于基础题．
练习册系列答案
相关题目
5．在△ABC中，已知$\overrightarrow{BC}$=3$\overrightarrow{BD}$，则$\overrightarrow{AD}$=（ ）
| A． | $\frac{1}{3}$（$\overrightarrow{AC}$+2$\overrightarrow{AB}$） | B． | $\frac{1}{3}$（$\overrightarrow{AB}$+2$\overrightarrow{AC}$） | C． | $\frac{1}{4}$（$\overrightarrow{AC}$+3$\overrightarrow{AB}$） | D． | $\frac{1}{4}$（$\overrightarrow{AC}$+2$\overrightarrow{AB}$） |
6．已知点P（x，y）的坐标满足条件$\left\{\begin{array}{l}{x-2y≤1}\\{x+4y≤4}\\{x+y≥a}\end{array}\right.$，当z=-2x+y取得最大值为1时，那么x2+y2的最小值为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
3．首项为正数的等差数列{an}满足5a6=3a3，则前n项和Sn中最大项为（ ）
| A． | S9 | B． | S10 | C． | S11 | D． | S12 |
20．车流量被定义为单位时间内通过的十字路口的车辆数，单位为辆/分，上班高峰期某十字路口的车流量有函数F（t）=60+3sin$\frac{t}{3}$（其中0≤t≤20）给出，F（t）的单位是辆/分，t的单位是分，则在下列哪个时间段内车流量是增加的（ ）
| A． | [15，20] | B． | [10，15] | C． | [5，10] | D． | [0，5] |
7．
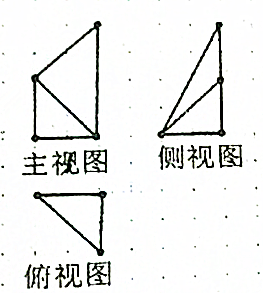某几何体的三视图如图所示，图中方格的长度为1，则几何体的体积为（ ）
某几何体的三视图如图所示，图中方格的长度为1，则几何体的体积为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
4．定义在R上的函数f（x）满足f（x）+$\sqrt{3}$f（$\frac{π}{2}$-x）=sinx，则f（$\frac{π}{12}$）=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |