题目内容
6.已知点P(x,y)的坐标满足条件$\left\{\begin{array}{l}{x-2y≤1}\\{x+4y≤4}\\{x+y≥a}\end{array}\right.$,当z=-2x+y取得最大值为1时,那么x2+y2的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 画出可行域$\left\{\begin{array}{l}{x-2y≤1}\\{x+4y≤4}\\{x+y≥a}\end{array}\right.$,当a≤1时,其可行域为△ABC,联立$\left\{\begin{array}{l}{x+y=a}\\{x+4y=4}\end{array}\right.$,解得M,当z=-2x+y取得最大值为1时,把Mz坐标代入解得a=1.那么x2+y2的最小值为原点O到直线x+y=1的距离的平方,利用点到直线的距离公式即可得出.
解答 解:画出可行域$\left\{\begin{array}{l}{x-2y≤1}\\{x+4y≤4}\\{x+y≥a}\end{array}\right.$,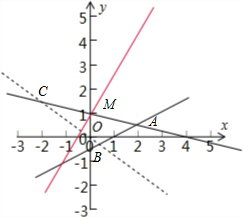
当a≤1时,其可行域为△ABC,
联立$\left\{\begin{array}{l}{x+y=a}\\{x+4y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{4a-4}{3}}\\{y=\frac{4-a}{3}}\end{array}\right.$,
当z=-2x+y取得最大值为1时,
可得1=$-2×\frac{4a-4}{3}$+$\frac{4-a}{3}$,
解得a=1.
那么x2+y2的最小值为原点O到直线x+y=1的距离的平方,
即x2+y2=$(\frac{|0-1|}{\sqrt{2}})^{2}$=$\frac{1}{2}$.
当a>1时,不满足条件,舍去.
故选:B.
点评 本题考查了线性规划的有关知识、直线的交点、点到直线的距离公式,考查了分类讨论思想方法、数形结合思想方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知f(x)=$\left\{\begin{array}{l}{-{x}^{2}-2x+3,x>0}\\{{x}^{2}-4x+3,x≤0}\end{array}\right.$,不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
| A. | (-∞,-2) | B. | (-∞,0) | C. | (0,2) | D. | (-2,0) |
11.已知集合A={x|y=ln(x2-x)},B={x|x2-9≤0},则A∩B=( )
| A. | [-3,0]∪[1,3] | B. | [-3,0)∪(1,3] | C. | (0,1) | D. | [-3,3] |
18.函数y=tan(x-$\frac{π}{3}$)+tanx+tan(x+$\frac{π}{3}$)的最小正周期是( )
| A. | $\frac{2π}{3}$ | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |