题目内容
3.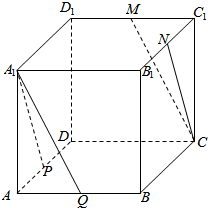 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:(1)A1P∥CN;
(2)A1Q∥CM;
(3)∠PA1Q=∠MCN.
分析 (1)可想着在A1P所在平面内,作CN的平行线,从而可取A1D1的中点N′,并连接NN′,DN′,从而可说明DN′∥CN,而容易得到A1P∥DN′,从而得出A1P∥CN;
(2)证明过程同(1),可取A1B1的中点M′,并连接BM′,MM′,从而可得到CM∥BM′,从而得出A1Q∥CM;
(3)对于本问的证明,可由定理:一个角度两边分别平行于另一个角的两边,这两个角相等或互补,得出.
解答 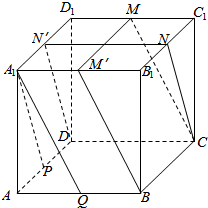 证明:(1)如图,取A1D1的中点N′,连接NN′,DN′;
证明:(1)如图,取A1D1的中点N′,连接NN′,DN′;
又N为B1C1中点;
∴NN′∥CD,且NN′=CD;
∴四边形CDN′N为平行四边形;
∴CN∥DN′;
∵P为AD中点;
∴四边形DPA1N′为平行四边形;
∴A1P∥DN′;
∴A1P∥CN;
(2)过程同上,取A1B1的中点M′,连接BM′,MM′,可得到四边形BCMM′为平行四边形,∴CM∥BM′;
又A1Q∥BM′;
∴A1Q∥CM;
(3)由(1)(2)知∠PA1Q的两边分别平行于∠MCN的两边;
∴∠PA1Q=∠MCN.
点评 考查平行四边形的定义及其判定,平行线的传递性,以及空间中一个角的两边分别平行于另一个角的两边,这两个角相等或互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知向量$\overrightarrow{a}$=(sinθ,-2)与$\overrightarrow{b}$=(1,cosθ)互相垂直,其中θ∈$(0,\frac{π}{2})$,则sinθ+cosθ等于( )
| A. | $\frac{{-\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |