题目内容
11.已知△ABC三条边长分别为a=t2+3,b=-t2-2t+3,c=4t则最大的内角度数为120°.分析 判断a,b,c的大小,确定出A为最大角,利用余弦定理求出cosA的值,即可确定出A的度数.
解答 解:∵△ABC三条边长分别为a=t2+3>3,b=-t2-2t+3=-(t+1)2+4<3,c=4t>0,即t>0,
∴a为最大边,即A为最大角,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{(-{t}^{2}-2t+3)^{2}+(4t)^{2}-({t}^{2}+3)^{2}}{2•(-{t}^{2}-2t+3)•4t}$=$\frac{4({t}^{3}+2{t}^{2}-3t)}{-8({t}^{3}+2{t}^{2}-3t)}$=-$\frac{1}{2}$,
则A=120°,
故答案为:120°
点评 此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
19.在复平面内,复数$\frac{1}{1+i}-\frac{1}{3}{i^7}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.若lg2=a,lg3=b,则log23等于( )
| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | ab | D. | ba |
16.设A,B,C,D是空间中的四个不同的点,则下列说法错误的是( )
| A. | 若AC与BD共面,则AD与BC也共面 | |
| B. | 若AC与BD是异面直线,则AD与BC也是异面直线 | |
| C. | 若AC与BD是相交直线,则AD与BC也是相交直线 | |
| D. | 若A,B,C,D不共面,则AC与BD既不平行也不相交 |
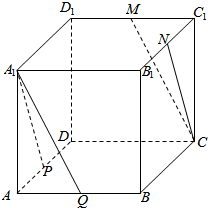 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证: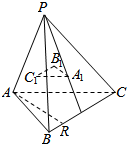 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.