题目内容
15.若a、b、x、y∈R+,且a+b=1,证明:ax2+by2≥(ax+by)2.分析 将所证的关系式作差(ax+by)2-(ax2+by2)=a(a-1)x2+b(b-1)y2+2abxy利用a+b=1,整理,可得a(a-1)x2+b(b-1)y2+2abxy=-ab(x-y)2≤0,当且仅当x=y时等号成立.
解答 证明:(ax+by)2-(ax2+by2)=a(a-1)x2+b(b-1)y2+2abxy,
因为a+b=1,
所以a-1=-b,b-1=-a,
又a,b均为正数,
所以a(a-1)x2+b(b-1)y2+2abxy=-ab(x2+y2-2xy)=-ab(x-y)2≤0,当且仅当x=y时等号成立.
所以ax2+by2≥(ax+by)2.
点评 本题考查不等式的证明,着重考查作差法的应用,突出考查等价转化思想与逻辑推理能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
6.若lg2=a,lg3=b,则log23等于( )
| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | ab | D. | ba |
4.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)在区间[-ω,ω]上单调递增,且函数f(x)的图象关于直线x=ω对称,则ω的值为( )
| A. | $\frac{\sqrt{π}}{3}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{3π}}{3}$ | D. | $\frac{\sqrt{3π}}{2}$ |
5.设$α=\frac{17}{3}π$,则( )
| A. | sinα>0,cosα>0 | B. | sinα<0,cosα<0 | C. | sinα>0,cosα<0 | D. | sinα<0,cosα>0 |
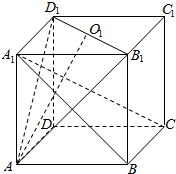 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.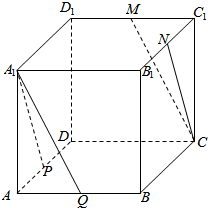 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证: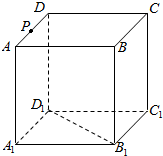 如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.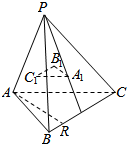 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.