题目内容
8．底面是菱形的直棱柱，若对角面的面积为50$\sqrt{2}$cm2和10$\sqrt{14}$cm2，而底边长为8cm，求该直棱柱的侧面积．分析 设侧棱长为l，两对角线分别为c，d，由条件建立方程组，消去c，d，用对角面的面积，求解表示侧面积．
解答 
解：设侧棱长为h，两对角线分别为c，d．
则$\left\{\begin{array}{l}ch=50\sqrt{2}\\ dh=10\sqrt{14}\\{（\frac{1}{2}c）}^{2}+{（\frac{1}{2}d）}^{2}=64\end{array}\right.$，可得c=$\frac{50\sqrt{2}}{h}$，
由（2）得d=$\frac{10\sqrt{14}}{h}$，代入${（\frac{1}{2}c）}^{2}+{（\frac{1}{2}d）}^{2}=64$得：${（\frac{25\sqrt{2}}{h}）}^{2}+{（\frac{5\sqrt{14}}{h}）}^{2}=64$，
∴64h2=625×2+25×14，∴S侧=4×8h=$\sqrt{1600}$=4×40=160．
直棱柱的侧面积：160．
点评 本题考查直四棱柱的定义、侧面积的求法，以及菱形的对角线的性质，属于中档题．
练习册系列答案
相关题目
19．在复平面内，复数$\frac{1}{1+i}-\frac{1}{3}{i^7}$对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
16．设A，B，C，D是空间中的四个不同的点，则下列说法错误的是（ ）
| A． | 若AC与BD共面，则AD与BC也共面 | |
| B． | 若AC与BD是异面直线，则AD与BC也是异面直线 | |
| C． | 若AC与BD是相交直线，则AD与BC也是相交直线 | |
| D． | 若A，B，C，D不共面，则AC与BD既不平行也不相交 |
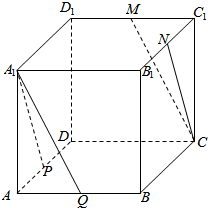在正方体ABCD-A1B1C1D1中，P，Q，M，N分别为AD，AB，C1D1，B1C1的中点，求证：
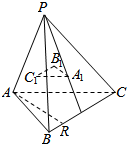如图，P是△ABC所在平面外的一点，A1，B1，C1依次是△PBC，△PAC，△PAB的重心，AR是平面ABC内的任意一条直线，求证：AR∥平面A1B1C1．