题目内容
12.若a2+b2=1,则-$\frac{1}{2}$≤ab≤$\frac{1}{2}$.分析 用参数法,设a=cosθ,b=sinθ,θ∈[0,2π),利用三角函数求出ab的最值即可.
解答 解:设a=cosθ,b=sinθ,θ∈[0,2π),
∴ab=cosθsinθ=$\frac{1}{2}$sin2θ,
又θ∈[0,2π),∴2θ∈[0,4π),
∴sin2θ∈[-1,1],
∴$\frac{1}{2}$sin2θ∈[-$\frac{1}{2}$,$\frac{1}{2}$],
ab∈[-$\frac{1}{2}$,$\frac{1}{2}$].
故答案为:-$\frac{1}{2}$,$\frac{1}{2}$.
点评 本题考查了单位圆的方程的应用问题,也考查了求最大最小值的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)在区间[-ω,ω]上单调递增,且函数f(x)的图象关于直线x=ω对称,则ω的值为( )
| A. | $\frac{\sqrt{π}}{3}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{3π}}{3}$ | D. | $\frac{\sqrt{3π}}{2}$ |
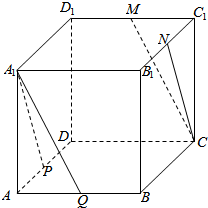 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证: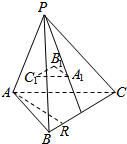 如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.
如图,P是△ABC所在平面外的一点,A1,B1,C1依次是△PBC,△PAC,△PAB的重心,AR是平面ABC内的任意一条直线,求证:AR∥平面A1B1C1.