题目内容
2.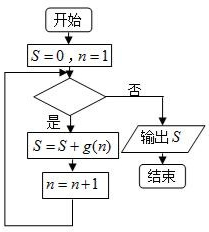 已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )| A. | n≤2014 | B. | n≤2015 | C. | n>2014 | D. | n>2015 |
分析 由已知中函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,可求出a值,进而求出函数f(x)及函数g(x)的解析式,然后利用裂项相消法,可求出g(1)+g(2)+g(3)+…+g(n)的值与n的关系,分析出最后进行循环的循环变量n的终值,分析后可得判断条件.
解答 解:∵函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,
故$\left\{\begin{array}{l}{3a>0}\\{f′(-1)=3a-1=0}\end{array}\right.$,
解得a=$\frac{1}{3}$,
∴f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$x2,
∴f′(x)=x2+x,
∴g(x)=$\frac{1}{f'(x)}$=$\frac{1}{{x}^{2}+x}$=$\frac{1}{x}$$-\frac{1}{x+1}$,
∴g(1)+g(2)+g(3)+…+g(n)=(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n}-\frac{1}{n+1}$)=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$,
所以当判断框内是“n≤2014?”时,输出结果为$\frac{2014}{2015}$.
若输出的结果S>$\frac{2014}{2015}$,
则表示累加的终值应满足n≤2015,
即n≤2015时,满足进入循环进行累加的条件,n>2015时退出循环
故选:B.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

 小题狂做系列答案
小题狂做系列答案| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{24}{7}$ | D. | -$\frac{24}{7}$ |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |

 如图,在△ABC中,∠B=$\frac{π}{3}$,点D在BC上,cos∠ADC=$\frac{1}{7}$,则cos∠BAD=$\frac{13}{14}$.
如图,在△ABC中,∠B=$\frac{π}{3}$,点D在BC上,cos∠ADC=$\frac{1}{7}$,则cos∠BAD=$\frac{13}{14}$.