题目内容
17.若实数x,y满足不等式组$\left\{\begin{array}{l}x+y-1≥0\\ 2x-y-2≤0\\ x-2y+2≥0\end{array}\right.$,则x-3y的最小值为-4,点P(x,y)所组成的平面区域的面积为$\frac{3}{2}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合进行求解即可.
解答 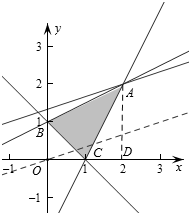 解:设z=x-3y,则得y=$\frac{1}{3}x-\frac{z}{3}$,
解:设z=x-3y,则得y=$\frac{1}{3}x-\frac{z}{3}$,
作出不等式组对应的平面区域如图(阴影部分):
平移直线y=$\frac{1}{3}x-\frac{z}{3}$,
由图象可知当直线y=$\frac{1}{3}x-\frac{z}{3}$经过点A时,直线y=$\frac{1}{3}x-\frac{z}{3}$的截距最大,
此时z最小,
由$\left\{\begin{array}{l}{2x-y-2=0}\\{x-2y+2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,即A(2,2).
将A(2,2)代入目标函数z=x-3y,
得z=2-3×2=2-6=-4.
∴目标函数z=x-3y的最小值是-4.
∵B(0,1),C(1,0),D(2,0),
∴△ABC的面积S=$\frac{(1+2)×2}{2}$-$\frac{1}{2}×1×1$$-\frac{1}{2}×1×2$=$\frac{3}{2}$,
故答案为:-4,$\frac{3}{2}$
点评 本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
5.下列说法不正确的是( )
| A. | 若“p且q”为假,则p、q至少有一个是假命题 | |
| B. | 命题“?x0∈R,x02-x0-1<0”的否定是“?x0∈R,x02-x0-1≥0” | |
| C. | “$φ=\frac{π}{2}$”是“y=sin (2x+φ) 为偶函数”的充要条件 | |
| D. | α<0时,幂函数y=xα在 (0,+∞) 上单调递减 |
12.为得到函数$y=sin(3x+\frac{π}{4})$的图象,只要把函数$y=sin(x+\frac{π}{4})$图象上所有的点( )
| A. | 横坐标缩短到原来的$\frac{1}{3}$倍,纵坐标不变 | |
| B. | 横坐标伸长到原来的3倍,纵坐标不变 | |
| C. | 纵坐标伸长到原来的3倍,横坐标不变 | |
| D. | 纵坐标缩短到原来的$\frac{1}{3}$倍,横坐标不变 |
2. 已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )
已知函数f(x)=ax3+$\frac{1}{2}{x^2}$的导函数为f′(x),且f(x)在x=-1处取得极大值,设g(x)=$\frac{1}{f'(x)}$,执行如图的程序框图,若输出的结果大于$\frac{2014}{2015}$,则判断框内可填入的条件是( )| A. | n≤2014 | B. | n≤2015 | C. | n>2014 | D. | n>2015 |
7.已知f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\left\{\begin{array}{l}cos\frac{πx}{6},0<x≤8\\ lo{g}_{2}x,x>8\end{array}\right.$,则f(f(-16))=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
