题目内容
【题目】将一铁块高温融化后制成一张厚度忽略不计、面积为100dm2的矩形薄铁皮(如图),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:
方案①:以![]() 为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;
为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;
方案②:以![]() 为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与
为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与![]() 或
或![]() 垂直)作为正四棱柱的两个底面.
垂直)作为正四棱柱的两个底面.
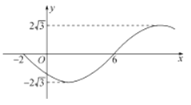
(1)设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;
(2)设![]() 的长为
的长为![]() dm,则当
dm,则当![]() 为多少时,能使按方案②制成的正四棱柱的体积最大?
为多少时,能使按方案②制成的正四棱柱的体积最大?

【答案】(1) 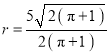 ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)设所得圆柱的半径为![]() ,根据矩形薄铁皮的面积为100
,根据矩形薄铁皮的面积为100![]() ,即可求得
,即可求得![]() 的值;(2)设所得正四棱柱的底面边长为
的值;(2)设所得正四棱柱的底面边长为![]()
![]() ,根据题意得
,根据题意得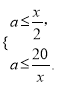 .方法一:表示出正四棱柱的体积
.方法一:表示出正四棱柱的体积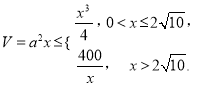 ,构造函数,求得单调性,即可求得函数的最大值,从而得体积最大值及
,构造函数,求得单调性,即可求得函数的最大值,从而得体积最大值及![]() 的值;方法二:表示出
的值;方法二:表示出![]() 的范围,从而得到
的范围,从而得到![]() 的范围,再表示出正四棱柱的体积,即可求得最大值及
的范围,再表示出正四棱柱的体积,即可求得最大值及![]() 的值.
的值.
试题解析:(1)设所得圆柱的半径为![]() ,则
,则![]() ,
,
解得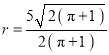 .
.
(2)设所得正四棱柱的底面边长为![]() dm,则
dm,则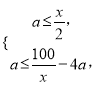 即
即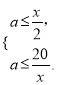
方法一:
所得正四棱柱的体积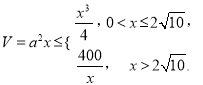
记函数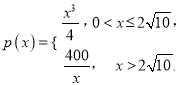 则
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时, ![]() .
.
∴当![]() ,
, ![]() 时,
时, ![]()
![]() dm3.
dm3.
方法二:
![]() ,从而
,从而![]() .
.
所得正四棱柱的体积![]() .
.
∴当![]() ,
, ![]() 时,
时, ![]()
![]() dm3.
dm3.
答:(1)圆柱的底面半径为 dm;
dm;
(2)当![]() 为
为![]() 时,能使按方案②制成的正四棱柱的体积最大.
时,能使按方案②制成的正四棱柱的体积最大.

【题目】某校为了解高一实验班的数学成绩,采用抽样调查的方式,获取了![]() 位学生在第一学期末的数学成绩数据,样本统计结果如下表:
位学生在第一学期末的数学成绩数据,样本统计结果如下表:
分组 | 频数 | 频率 |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
合计 |
|
|
(1)求![]() 的值和实验班数学平均分的估计值;
的值和实验班数学平均分的估计值;
(2)如果用分层抽样的方法从数学成绩小于![]() 分的学生中抽取
分的学生中抽取![]() 名学生,再从这
名学生,再从这![]() 名学生中选
名学生中选![]() 人,求至少有一个学生的数学成绩是在
人,求至少有一个学生的数学成绩是在![]() 的概率.
的概率.