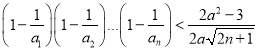题目内容
【题目】![]() 是坐标原点,椭圆
是坐标原点,椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,若
在椭圆上,若![]() 的面积最大时
的面积最大时![]() 且最大面积为
且最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,点
,点![]() 是第四象限内的点且在椭圆
是第四象限内的点且在椭圆![]() 上,线段
上,线段![]() 被直线
被直线![]() 垂直平分,直线
垂直平分,直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;
;
(2)证明见解析.
【解析】
(1)由![]() 的面积最大时
的面积最大时![]() 且最大面积为
且最大面积为![]() 求得
求得![]() 且
且![]() ,再结合
,再结合![]() 即可求出椭圆
即可求出椭圆![]() 的标准方程;(2)易知
的标准方程;(2)易知![]() ,设直线
,设直线![]() :
:![]() ,则直线
,则直线![]() :
:![]() ,然后分别与
,然后分别与![]() 联立求出
联立求出![]() ,
,![]() ,再利用斜率公式得出
,再利用斜率公式得出![]() 的值即可.
的值即可.
(1)当![]() 是椭圆的上顶点或下顶点时
是椭圆的上顶点或下顶点时![]() 的面积最大,设
的面积最大,设![]() 是椭圆的上顶点,
是椭圆的上顶点,
则![]() 即
即![]() ,
,
又![]() ,
,![]() ∴
∴![]() ,
,![]() ,
,![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)依题意点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 不与
不与![]() 垂直,设直线
垂直,设直线![]() :
:![]() ,
,
即![]() ,直线
,直线![]() :
:![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
由 得
得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
则![]() .
.
又![]() ,
,![]() ,
,
∴![]()
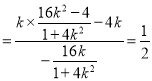 ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目