题目内容
已知函数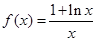 .
.
(1)若函数 在区间
在区间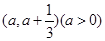 上存在极值点,求实数
上存在极值点,求实数 的取值范围;
的取值范围;
(2)当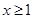 时,不等式
时,不等式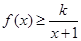 恒成立,求实数
恒成立,求实数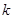 的取值范围;
的取值范围;
(3)求证: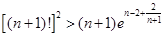 .(
.(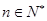 ,
,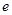 为自然对数的底数)
为自然对数的底数)
(1) 实数 的取值范围为
的取值范围为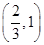 ;(2)
;(2)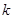 的取值范围为
的取值范围为 ;(3) 见解析.
;(3) 见解析.
解析试题分析:(1)先利用导数求出函数在 处取得唯一的极值,因为函数
处取得唯一的极值,因为函数 在区间
在区间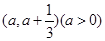 上
上 存在极值点,故
存在极值点,故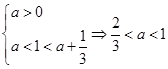 ;(2)根据条件可得
;(2)根据条件可得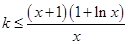 ,然后令
,然后令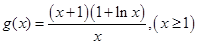 ,求出
,求出 的最小值,即可解得
的最小值,即可解得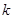 的范围;(3)由(2)的结论可得
的范围;(3)由(2)的结论可得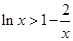 ,令
,令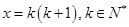 ,则有
,则有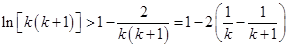 ,分别令
,分别令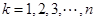 ,
,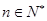 则有
则有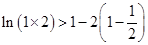

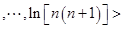
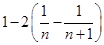 将这
将这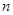 个不等式左右两边分别相加可得
个不等式左右两边分别相加可得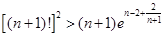 .
.
试题解析:(1)函数 定义域为
定义域为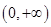 ,
,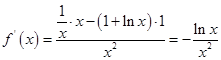 ,
,
由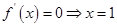 ,当
,当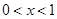 时,
时,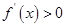 ,当
,当 时,
时,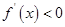 ,
,
则 在
在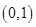 上单增,在
上单增,在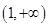 上单减,函数
上单减,函数 在
在 处取得唯一的极值。
处取得唯一的极值。
由题意得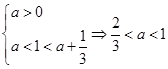 ,故所求实数
,故所求实数 的取值范围为
的取值范围为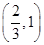 4分
4分
(2) 当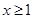 时,不等式
时,不等式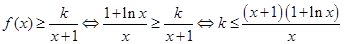 . 6分
. 6分
令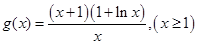 ,由题意,
,由题意,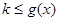 在
在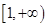 恒成立。
恒成立。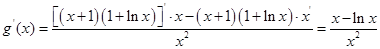
令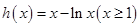 ,则
,则 ,当且仅当
,当且仅当 时取等号。
时取等号。
所以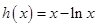 在
在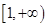 上单调递增,
上单调递增,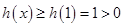
因此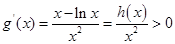 ,则
,则 在
在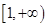 上单调递增,
上单调递增,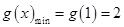
所以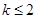 ,即实数
,即实数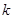 的取值范围为
的取值范围为 9分
9分
(3)由(2)知,当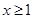 时,不等式
时,不等式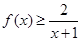 恒成立,
恒成立,
即 , 11分
, 11分
令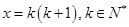 ,则有
,则有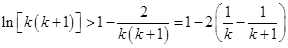 .
.
分别令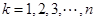 ,
,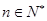 则有
则有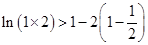 ,
,
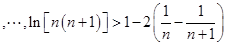 将这
将这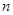 个不等式左右两边分别相加,则得
个不等式左右两边分别相加,则得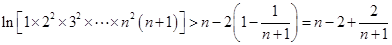
故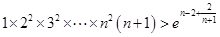 ,从而
,从而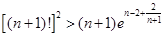 .
. 14分
14分
考点:1.利用导数求函数的极值;2.利用函数单调性解参数范围;3.对数式的运算性质;4.不等式证明.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

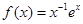 的定义域为
的定义域为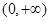 .
.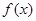 在
在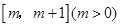 上的最小值;
上的最小值;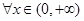 ,不等式
,不等式 恒成立,求
恒成立,求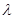 的取值范围.
的取值范围.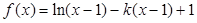 .
.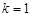 时,求函数
时,求函数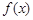 的最大值;
的最大值;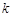 的取值范围;
的取值范围;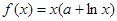 有极小值
有极小值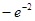 .
.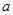 的值;
的值;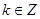 ,且
,且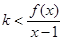 对任意
对任意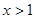 恒成立,求
恒成立,求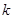 的最大值为.
的最大值为.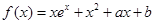 在点
在点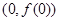 处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+
处的切线方程是x+ y-l=0,其中e为自然对数的底数,函数g(x)=1nx- cx+ 1+ c(c>0),对一切x∈(0,+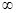 )均有
)均有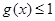 恒成立.
恒成立.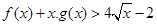 .
.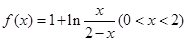 .
.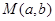 ,使得函数
,使得函数 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数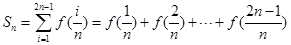 ,其中
,其中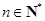 ,求
,求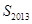 ;
;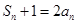 ,若不等式
,若不等式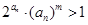 对
对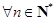 且
且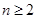 恒成立,求实数
恒成立,求实数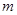 的取值范围.
的取值范围.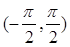 的函数
的函数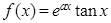
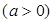 ,在
,在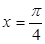 处的切线斜率为
处的切线斜率为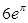
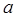 及
及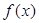 的单调区间;
的单调区间;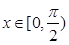 时,
时, 恒成立,求
恒成立,求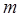 的取值范围.
的取值范围.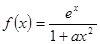 ,其中
,其中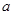 为正实数,
为正实数,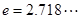 .
.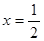 是
是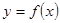 的一个极值点,求
的一个极值点,求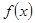 的单调区间.
的单调区间.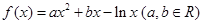
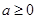 ,求
,求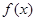 的单调区间;
的单调区间;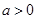 ,且对于任意
,且对于任意 ,
,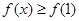 .试比较
.试比较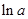 与
与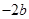 的大小.
的大小.