题目内容
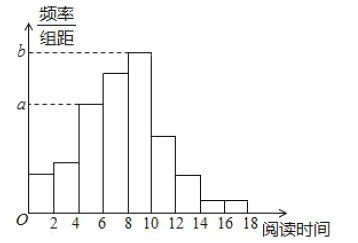
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
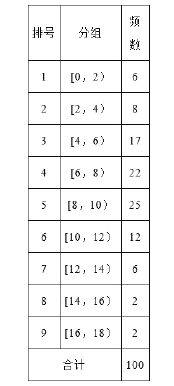
(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(Ⅱ)求频率分布直方图中的![]() 的值;
的值;
(Ⅲ)从阅读时间在![]() 的学生中任选2人,求恰好有1人阅读时间在
的学生中任选2人,求恰好有1人阅读时间在![]() ,另1 人阅读时间在
,另1 人阅读时间在![]() 的概率.
的概率.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用频率估计概率,由频率分布直方图得课外阅读不少于12小时的学生数,然后除以100即可;(2)利用![]() 进行求解,可得
进行求解,可得![]() ;(3)由频率分布直方图可得阅读时间在
;(3)由频率分布直方图可得阅读时间在![]() 的学生共4人,其中阅读时间落在
的学生共4人,其中阅读时间落在![]() 的有2人,阅读时间落在
的有2人,阅读时间落在![]() 的有2人,用列举法得到所有可能的试验结果,根据古典概型概率公式求解。
的有2人,用列举法得到所有可能的试验结果,根据古典概型概率公式求解。
试题解析:
(1)由频率分布直方图知,100名学生中课外阅读不少于12小时的学生共有10名,所以样本中课外阅读时间少于12小时的的频率是![]() .
.
(2)课外阅读时间落在![]() 的有17人,频率为0.17,
的有17人,频率为0.17,
所以![]()
课外阅读时间落在![]() 的有25人,频率为0.25,
的有25人,频率为0.25,
所以![]()
(3)课外阅读时间落在![]() 的有2人设为
的有2人设为![]() ;课外阅读时间落在
;课外阅读时间落在![]() 的有2人设为
的有2人设为![]() ,
,
则从课外阅读时间落在![]() 的学生中任选2人包含
的学生中任选2人包含![]() 共 6 种,
共 6 种,
其中恰好有1人阅读时间在![]() ,另1人阅读时间在
,另1人阅读时间在![]() 的有
的有![]() 共 4 种,
共 4 种,
所以所求概率为![]() ,
,
即恰好有1人阅读时间在![]() ,另1 人阅读时间在
,另1 人阅读时间在![]() 的概率为
的概率为![]() .
.

【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()