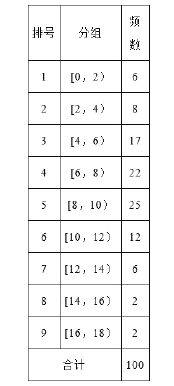
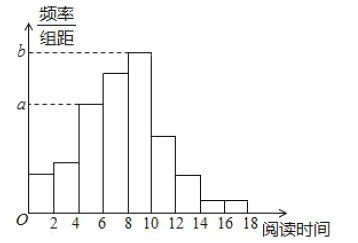
题目内容
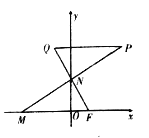
【题目】已知点![]() ,动点
,动点![]() ,
, ![]() 分别在
分别在![]() 轴,
轴, ![]() 轴上运动,
轴上运动, ![]() ,
, ![]() 为平面上一点,
为平面上一点, ![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
(Ⅰ)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点(直线
两点(直线![]() 不过
不过![]() ),交
),交![]() 于
于![]() ,
, ![]() 两点.若线段
两点.若线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】试题分析:(Ⅰ)由题意可得![]() 为
为![]() ,
, ![]() 的中点,设
的中点,设![]() ,则
,则![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,结合
,结合![]() 可得点
可得点![]() 的轨迹方程;(Ⅱ)设直线
的轨迹方程;(Ⅱ)设直线![]() 与
与![]() 轴的交点
轴的交点![]() ,设
,设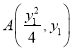 ,
, 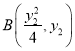 ,
, ![]() ,
, ![]() 中点为
中点为![]() , 当当
, 当当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 可得
可得![]() ,当
,当![]() 与
与![]() 轴垂直时也适合方程,由题意得
轴垂直时也适合方程,由题意得![]() 即为
即为![]() 的准线,结合面积公式即可.
的准线,结合面积公式即可.
试题解析:(Ⅰ)设![]() ,由
,由![]() 为
为![]() ,
, ![]() 的中点可得
的中点可得![]() 为
为![]() ,
, ![]() 的中点,则
的中点,则![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
,![]() ,
, ![]()
![]() 可得点
可得点![]() 的轨迹方程为:
的轨迹方程为: ![]()
(Ⅱ)设直线![]() 与
与![]() 轴的交点
轴的交点![]() ,设
,设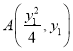 ,
, 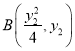
设![]() ,
, ![]() 中点为
中点为![]() ,
,
当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 可得
可得![]()
而![]() ,则
,则![]() 即
即![]() ,即
,即![]()
当![]() 与
与![]() 轴垂直时,
轴垂直时, ![]() ,
, ![]() 中点
中点![]() 与
与![]() 重合,适合方程.
重合,适合方程.
由![]() 为
为![]() ,
, ![]() 的中点,可知过
的中点,可知过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() 即为
即为![]() 的准线,
的准线,
![]() ,
, ![]()
![]()
![]() 与
与![]() 的面积之比为2.
的面积之比为2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目