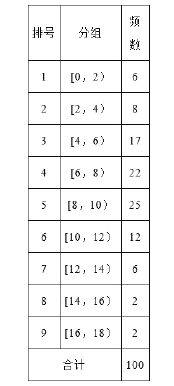
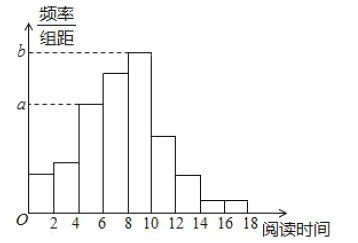
题目内容
【题目】已知函数f(n)=n2sin ![]() ),且an=f(n)+f(n+1),则a1+a2+a3+…+a2016的值为
),且an=f(n)+f(n+1),则a1+a2+a3+…+a2016的值为
【答案】4023
【解析】解:∵f(n)=n2sin ![]() ),
),
∴f(1)=1,f(2)=0,f(3)=﹣32 , f(4)=0,…,
可得f(2k)=4k2sinkπ=0,k∈N* , f(2k﹣1)=(2k﹣1)2 ![]() =(2k﹣1)2(﹣1)k﹣1 .
=(2k﹣1)2(﹣1)k﹣1 .
又an=f(n)+f(n+1),
∴a2k﹣1=f(2k﹣1)+f(2k)=(2k﹣1)2(﹣1)k﹣1 , a2k=f(2k)+f(2k+1)=(2k+1)2(﹣1)k .
∴a2k﹣1+a2k=(2k﹣1)2(﹣1)k﹣1+(2k+1)2(﹣1)k=(﹣1)k8k.
则a1+a2+a3+…+a2016=8×[﹣1+2﹣3+4+…﹣1007+1008]=4032.﹣.
所以答案是:4032.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系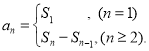 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目