题目内容
【题目】已知![]() 为实数,用
为实数,用![]() 表示不超过
表示不超过![]() 的最大整数.
的最大整数.
(1)若函数![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() ,求
,求![]() 的值域;
的值域;
(3)若存在![]() 且
且![]() ,使得
,使得![]() ,则称函数
,则称函数![]() 是
是![]() 函数,若函数
函数,若函数 ![]() 是
是![]() 函数,求
函数,求![]() 的取值范围.
的取值范围.
【答案】(1)1,2;(2){0,1};(3)![]() 且
且![]() 且
且![]() .
.
【解析】
(1)根据取整函数的定义直接计算;
(2)考虑![]() 与
与![]() 之间的大小关系,从而得到
之间的大小关系,从而得到![]() 的值域;
的值域;
(3)对![]() 进行分类讨论:
进行分类讨论:![]() ,利用单调性证明
,利用单调性证明![]() 在
在![]() 时不成立,当
时不成立,当![]() 时,再对
时,再对![]() 分类讨论:
分类讨论:![]() ,由此求解出
,由此求解出![]() 的取值范围.
的取值范围.
(1)f(1.2)=1,f(-1.2)=-2;
(2)因为[![]() ]=[
]=[![]() ]或[
]或[![]() ]=[
]=[![]() ]+1
]+1
所以若函数![]() 的值域为{0,1}
的值域为{0,1}
(3)当函数f(x)=x+![]() 是Ω函数时,
是Ω函数时,
若a=0,则f(x)=x显然不是Ω函数,矛盾.
若a<0,则![]() 是一个增函数,
是一个增函数,
所以f(x)在(﹣∞,0),(0,+∞)上单调递增,
此时不存在m<0,使得f(m)=f([m]),
同理不存在m>0,使得f(m)=f([m]),
又注意到m[m]≥0,即不会出现[m]<0<m的情形,
所以此时f(x)=x+![]() 不是Ω函数.
不是Ω函数.
当a>0时,设f(m)=f([m]),所以m+![]() =[m]+
=[m]+![]() ,所以有a=m[m],其中[m]≠0,
,所以有a=m[m],其中[m]≠0,
当m>0时,
因为[m]<m<[m]+1,所以[m]2<m[m]<([m]+1)[m],
所以[m]2<a<([m]+1)[m],
当m<0时,[m]<0,
因为[m]<m<[m]+1,所以[m]2>m[m]>([m]+1)[m],
所以[m]2>a>([m]+1)[m],
记k=[m],综上,我们可以得到:a>0且k∈N,a≠k2且a≠k(k+1).

【题目】某纪念章从2018年10月1日起开始上市,通过市场调查,得到该纪念章每1枚的市场价(单位:元)与上市时间(单位:天)的数据如下:
上市时间 | 4 | 10 | 36 |
市场价 | 90 | 51 | 90 |
(1)根据上表数据,从下列函数中选取一个恰当的函数描述该纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系并说明理由:①
的变化关系并说明理由:①![]() ;②
;②![]() ;③
;③![]() .
.
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
【题目】2017年11月、12月全国大范围流感爆发,为研究昼夜温差大小与患感冒人数多少之间的关系,一兴趣小组抄录了某医院11月到12月间的连续6个星期的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率;
(Ⅱ)若选取的是第一周与第六周的两组数据,请根据第二周到第五周的4组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: 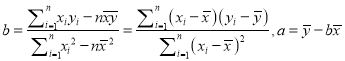 )
)
参考数据: ![]() 1092,
1092, ![]() 498
498
