题目内容
设f(x)是定义在R上的奇函数,当x<0时,f′(x)>0,且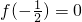 ,则不等式f(x)<0的解集为________.
,则不等式f(x)<0的解集为________.
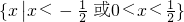
分析:由函数f(x)是定义在R上的奇函数,
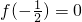 ,则
,则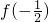 =f(0)=f(
=f(0)=f( )=0,则可以将定义域R分为(-∞,-1),(-1,0),(0,1),(1,+∞)四个区间结合单调性进行讨论,可得答案.
)=0,则可以将定义域R分为(-∞,-1),(-1,0),(0,1),(1,+∞)四个区间结合单调性进行讨论,可得答案.解答:∵当x<0时,f′(x)>0,∴f(x)在(-∞,0)上为减函数,
∵
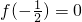
∴不等式f(x)<0的解集为
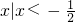 ,
,∵f(x)是定义在R上的奇函数,
∴f(x)在(0,+∞)上为增函数,且f(
 )=0,
)=0,∴不等式f(x)<0的解集为
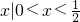 ,
,综上不等式f(x)<0的解集为
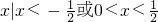
故答案为:
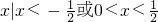 .
.点评:解答本题的关键是根据已知条件,结合奇函数的性质,找出函数的零点,并以零点为端点将定义域分为几个不同的区间,然后在每个区间上结合函数的单调性进行讨论,这是分类讨论思想在解决问题的巨大作用的最好体现,分类讨论思想往往能将一个复杂的问题的简单化,是高中阶段必须要掌握的一种方法.属中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |