题目内容
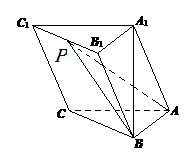
如图,在三棱柱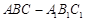 中,
中,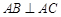 ,顶点
,顶点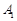 在底面
在底面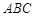 上的射影恰为点
上的射影恰为点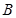 ,
,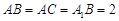 .
.
(1)证明:平面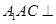 平面
平面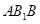 ;
;
(2 )若点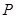 为
为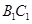 的中点,求出二面角
的中点,求出二面角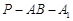 的余弦值.
的余弦值.
(1)证明:平面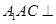 平面
平面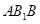 ;
;
(2)若点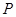 为
为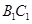 的中点,求出二面角
的中点,求出二面角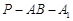 的余弦值.
的余弦值.
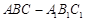 中,
中,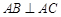 ,顶点
,顶点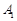 在底面
在底面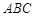 上的射影恰为点
上的射影恰为点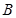 ,
,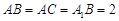 .
.(1)证明:平面
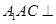 平面
平面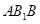 ;
; (2 )若点
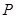 为
为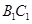 的中点,求出二面角
的中点,求出二面角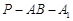 的余弦值.
的余弦值.
(1)证明:平面
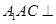 平面
平面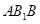 ;
; (2)若点
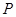 为
为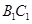 的中点,求出二面角
的中点,求出二面角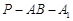 的余弦值.
的余弦值.(1)证明详见解析;(2)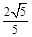
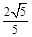
试题分析:(1)根据直线与平面垂直的性质可得
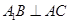 ,而已知
,而已知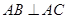 ,由直线与平面垂直的判定定理可得
,由直线与平面垂直的判定定理可得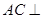 面
面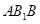 ,根据平面与平面垂直的判定定理可得平面
,根据平面与平面垂直的判定定理可得平面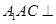 平面
平面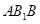 ;
; (2) 过P做PP1//A1B1交A1C1的中点于P1,由(1)可知P1A1
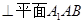 ,连接P1B,则
,连接P1B,则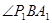 为二面角
为二面角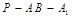 的平面角, 解
的平面角, 解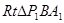 可得cos
可得cos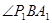 的值.
的值.试题解析:证明:(1)由题意得:
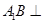 面
面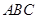 ,
,∴
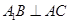 , 2分
, 2分又
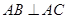 ,
,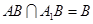
∴
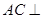 面
面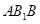 , 3分
, 3分∵
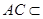 面
面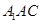 , ∴平面
, ∴平面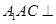 平面
平面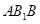 ; 5分
; 5分(2)解法1:以A为原点,建立如图所示的空间直角坐标系,
则
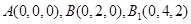
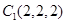
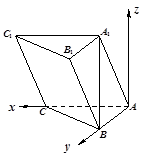
因为P为棱
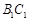 的中点,故易求得
的中点,故易求得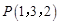 . 6分
. 6分 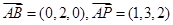
设平面
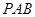 的法向量为
的法向量为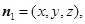
则
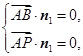 得
得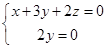
令
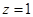 ,则
,则 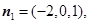 8分
8分 而平面
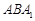 的法向量
的法向量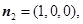 9分
9分 则
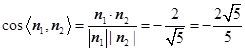 11分
11分由图可知二面角
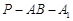 为锐角,
为锐角,故二面角
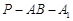 的平面角的余弦值是
的平面角的余弦值是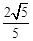 . 12分
. 12分 解法2:过P做PP1//A1B1交A1C1的中点于P1,由(1)可知P1A1
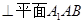 ,连接P1B,则
,连接P1B,则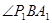 为二面角
为二面角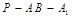 的平面角, 8分
的平面角, 8分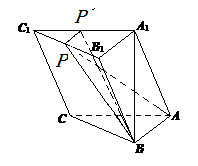
在
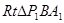 中,
中,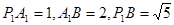 ,
,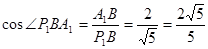 ,
,故二面角
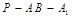 的平面角的余弦值是
的平面角的余弦值是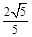 12分
12分 
练习册系列答案
相关题目
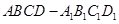 中,底面ABCD和侧面
中,底面ABCD和侧面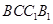 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,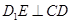 ,
,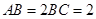 .
.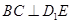 ;
;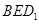 所成的锐二面角的大小为
所成的锐二面角的大小为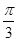 ,求线段
,求线段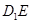 的长度.
的长度.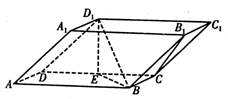
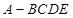 ,
,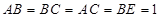 ,
,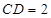 ,
,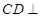 平面
平面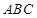 ,
,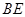 ∥
∥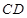 ,
,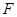 为
为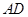 的中点.
的中点.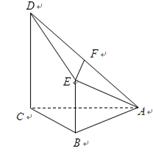
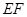 ∥平面
∥平面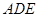
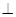 平面
平面 ;
;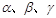 为平面,
为平面,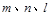 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为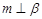 的一个充分条件的是( )
的一个充分条件的是( )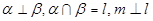
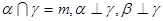
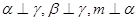
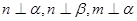
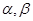 为两个不同的平面,则下列说法正确的是( )
为两个不同的平面,则下列说法正确的是( )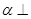 平面
平面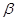 的一个充分条件是
的一个充分条件是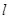 ,
, 且
且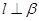
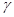 ,
,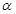 且
且