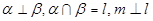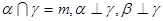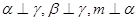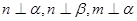题目内容
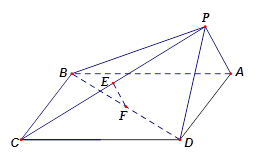
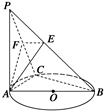
如图,在四棱锥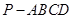 中,底面
中,底面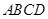 是正方形,侧面
是正方形,侧面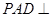 底面
底面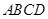 .
.
(Ⅰ)若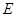 ,
, 分别为
分别为 ,
, 中点,求证:
中点,求证: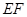 ∥平面
∥平面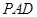 ;
;
(Ⅱ)求证: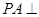
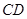 ;
;
(Ⅲ)若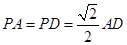 ,求证:平面
,求证:平面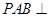 平面
平面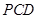 .
.
 中,底面
中,底面 是正方形,侧面
是正方形,侧面 底面
底面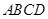 .
.(Ⅰ)若
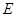 ,
, 分别为
分别为 ,
, 中点,求证:
中点,求证: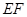 ∥平面
∥平面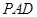 ;
;(Ⅱ)求证:
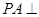
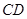 ;
;(Ⅲ)若
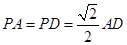 ,求证:平面
,求证:平面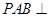 平面
平面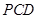 .
.
(Ⅰ)详见解析,(Ⅱ)详见解析,(Ⅲ)详见解析.
试题分析:(Ⅰ)证明线面平行,关键在于找出线线平行.本题条件含中点,故从中位线上找线线平行.
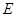 ,
, 分别为
分别为 ,
, 中点,在△
中点,在△ 中,
中,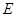 是
是 中点,
中点, 是
是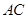 中点,所以
中点,所以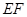 ∥
∥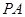 .又因为
.又因为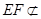 平面
平面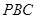 ,
,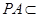 平面
平面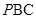 ,所以
,所以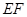 ∥平面
∥平面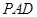 .(Ⅱ)由面面垂直性质定理可得线面垂直,因为平面
.(Ⅱ)由面面垂直性质定理可得线面垂直,因为平面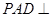 底面
底面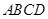 ,且平面
,且平面 平面
平面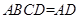 ,又
,又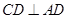 ,
,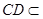 平面
平面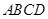 ,所以
,所以 面
面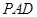 .又因为
.又因为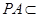 平面
平面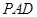 ,所以
,所以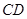
 .即
.即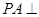
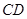 .(Ⅲ)证明面面垂直,关键找出线面垂直. 在△
.(Ⅲ)证明面面垂直,关键找出线面垂直. 在△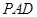 中,因为
中,因为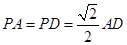 ,所以
,所以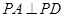 .由(Ⅱ)可知
.由(Ⅱ)可知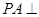
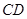 ,且
,且 ,
,所以
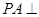 平面
平面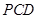 .又因为
.又因为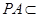 平面
平面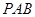 ,所以平面
,所以平面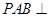 平面
平面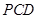 .
.证明:(Ⅰ)如图,连结
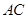 .
.因为底面
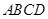 是正方形,
是正方形,所以
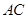 与
与 互相平分.
互相平分. 又因为
 是
是 中点,
中点,所以
 是
是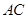 中点.
中点.在△
 中,
中,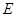 是
是 中点,
中点, 是
是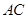 中点,
中点,所以
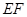 ∥
∥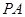 .
.又因为
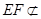 平面
平面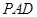 ,
,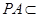 平面
平面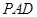 ,
,所以
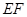 ∥平面
∥平面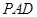 . 4分
. 4分(Ⅱ)因为平面
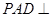 底面
底面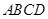 ,且平面
,且平面 平面
平面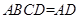 ,
,又
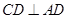 ,
,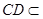 平面
平面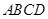 ,
,所以
 面
面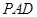 .
.又因为
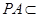 平面
平面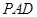 ,
,所以
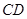
 .即
.即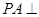
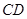 . 9分
. 9分 (Ⅲ)在△
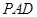 中,因为
中,因为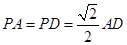 ,所以
,所以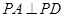 .
.由(Ⅱ)可知
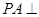
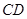 ,且
,且 ,
,所以
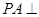 平面
平面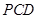 .
.又因为
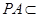 平面
平面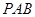 ,
,所以平面
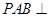 平面
平面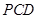 . 14分
. 14分 
练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
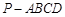 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中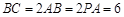 ,
,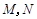 为侧棱
为侧棱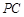 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.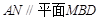 ;
;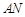 与
与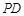 所成角的余弦值;
所成角的余弦值;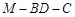 的余弦值.
的余弦值.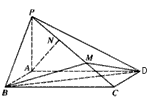
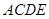 所在的平面与平面
所在的平面与平面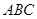 垂直,
垂直,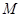 是
是 和
和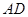 的交点,
的交点,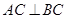 ,且
,且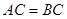 .
.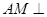 平面
平面 ;
; 的大小.
的大小.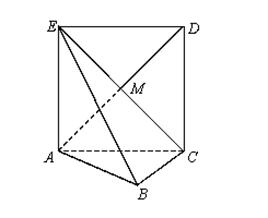
 中,四边形
中,四边形 是菱形,四边形
是菱形,四边形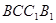 是矩形,
是矩形,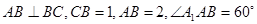 .
.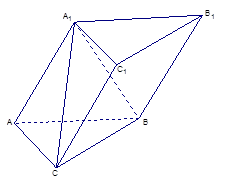
 ;
;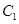 到平面
到平面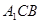 的距离;
的距离;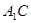 与平面
与平面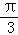 ,F为PC的中点,AF⊥PB.
,F为PC的中点,AF⊥PB.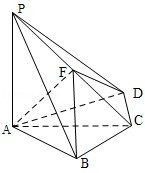
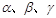 为平面,
为平面,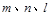 为直线,以下四组条件,可以作为
为直线,以下四组条件,可以作为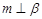 的一个充分条件的是( )
的一个充分条件的是( )