Question

【题目】已知函数f（x）=lnx．
（1）设h（x）为偶函数，当x＜0时，h（x）=f（﹣x）+2x，求曲线y=h（x）在点（1，﹣2）处的切线方程；
（2）设g（x）=f（x）﹣mx，求函数g（x）的极值；
（3）若存在x0＞1，当x∈（1，x0）时，恒有f（x）＞ 成立，求实数k的取值范围．

Answer 1

【答案】
（1）解：x＜0时，h（x）=f（﹣x）+2x，h（x）是偶函数，

故h（x）=lnx﹣2x，（x＞0），

h′（x）= ﹣2，故h′（1）=﹣1，

故切线方程是：y+2=﹣（x﹣1），

即x+y+1=0

（2）解：g（x）=lnx﹣mx，（x＞0），

g′（x）= ﹣m，

m≤0时，g′（x）＞0，g（x）在（0，+∞）递增，函数无极值，

m＞0时，令g′（x）＞0，解得：0＜x＜ ，令g′（x）＜0，解得：x＞ ，

故g（x）在（0， ）递增，在（ ，+∞）递减，

故g（x）的最大值是g（ ）=﹣lnm﹣1；无极小值

（3）证明：设g（x）=f（x）﹣ x2﹣（k﹣1）x+k﹣ ，x∈（1，+∞），

则g′（x）= ，

当x＞1时，g′（x）＜0，所以g（x）在（1，+∞）上单调递减，

所以当x＞1时，g（x）＜g（1）=0，

即当x＞1时，f（x）＜x﹣1；

①当k=1时，由（2）知，当x＞1时，f（x）＜x﹣1，

此时不存在x0＞1，不满足题意；

②当k＞1时，x＞1，f（x）＜x﹣1＜k（x﹣1），

此时不存在x0＞1，不满足题意；

③当k＜1时，设h（x）=f（x）﹣k（x﹣1），x＞1，

则h′（x）= ，

令h′（x）=0，即﹣x2+（1﹣k）x+1=0，

得x1= 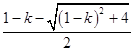＜0，x2= 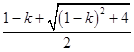＞1，

所以当x∈（1，x2）时，h′（x）＞0，所以h（x）在[1，x2）上单调递增，

取x0=x2，所以当x∈（1，x0）时，h（x）＞h（1）=0，f（x）＞k（x﹣1），

综上，实数k的取值范围是（﹣∞，1）

【解析】（1）求出h（x）的解析式，求出函数的导数，计算h′（1）的值，求出切线方程即可；（2）求出g（x）的导数，通过讨论m的范围，求出函数的单调区间，从而求出函数的极值即可；（3）通过讨论k的范围，求出函数的单调性，结合题意求出k的范围即可．
【考点精析】本题主要考查了函数的极值与导数的相关知识点，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值才能正确解答此题．