Question

【题目】已知函数f（α）=
（1）化简f（α）；
（2）若f（α）= ＜α＜0，求sinαcosα，sinα﹣cosα的值．

Answer 1

【答案】
（1）解：f（α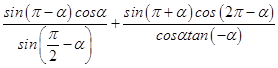）= = + =sinα+cosα= sin（α+ ）
（2）解：由 ，平方可得 ，

即 ，∴sinαcosα=﹣ ，∵（sinα﹣cosα）2=1﹣2sinαcosα= ，

又 ，所以sinα＜0，cosα＞0，所以sinα﹣cosα＜0，∴sinα﹣cosα=﹣

【解析】（1）利用诱导公式化简三角函数式f（α）的解析式，可得结果．（2）利用同角三角函数的基本关系求得 sinαcosα 的值，结合 sinα与cosα 的符号，可得（sinα﹣cosα）2的值，可得sinα﹣cosα的值．