题目内容
【题目】如图,长方体ABCD﹣A1B1C1D1中,AA1=AB=2,AD=1点E,F,G分别是DD1 , AB,CC1的中点,则异面直线A1E与GF所成的角是( ) 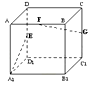
A.90°
B.60°
C.45°
D.30°
【答案】A
【解析】解:由题意:ABCD﹣A1B1C1D1是长方体,E,F,G分别是DD1,AB,CC1的中点,连接B1G,
∵A1E∥B1G,
∴∠FGB1为异面直线A1E与GF所成的角.
连接FB1,
在三角形FB1G中,AA1=AB=2,AD=1,
B1F= ![]() =
= ![]()
B1G= ![]() =
= ![]() ,
,
FG= ![]() =
= ![]() ,
,
B1F2=B1G2+FG2.
∴∠FGB1=90°,
即异面直线A1E与GF所成的角为90°.
故选A.

【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.

练习册系列答案
相关题目
【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量,现从武汉市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以这100个人的样本数据估计武汉市的总体数据且以频率估计概率,若从全市大学生(数量很大)中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望.
