题目内容
18.已知函数f(x)=mx+$\frac{n}{x}$以(1,a)为切点的切线方程是3x+y-8=0.(Ⅰ)求实数m,n的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)求函数f(x)切线倾斜角α的取值范围.
分析 (Ⅰ)根据切线方程能够求出切点(1,5),求f′(x)=m-$\frac{n}{{x}^{2}}$,从而根据切线斜率及切点在f(x)上可得到$\left\{\begin{array}{l}{m+n=5}\\{m-n=-3}\end{array}\right.$,解方程组即得m=1,n=4;
(Ⅱ)上面求出了m,n,从而得出f′(x)=$\frac{{x}^{2}-4}{{x}^{2}}$,根据导数符号即可判断函数f(x)的单调性,从而求出f(x)的单调区间;
(Ⅲ)由f′(x)=$1-\frac{4}{{x}^{2}}$便知tanα=$1-\frac{4}{{x}^{2}}<1$,结合正切函数的图象即可写出切线倾斜角α的取值范围.
解答 解:(Ⅰ)切点(1,a)在切线3x+y-8=0上;
∴3+a-8=0;
∴a=5;
∴切点为(1,5);
又f′(x)=m$-\frac{n}{{x}^{2}}$,切点在函数f(x)的图象上,切线方程斜率为k=-3;
∴$\left\{\begin{array}{l}{m+n=5}\\{m-n=-3}\end{array}\right.$;
解得m=1,n=4;
(Ⅱ)由(Ⅰ)知,$f′(x)=\frac{(x+2)(x-2)}{{x}^{2}}$;
∴x<-2时,f′(x)>0,-2<x<0时,f′(x)<0,0<x<2时,f′(x)<0,x>2时,f′(x)>0;
∴f(x)的单调增区间为(-∞,-2],[2,+∞),单调减区间为(-2,0),(0,2);
(Ⅲ)由(Ⅰ)知,$f′(x)=1-\frac{4}{{x}^{2}}<1$;
∴tanα<1;
∴函数f(x)切线倾斜角α的取值范围是[$0,\frac{π}{4}$)∪($\frac{π}{2},π$).
点评 考查过f(x)上一点的切线的斜率和函数f(x)在该点处的导数的关系,以及根据导数符号求函数单调区间的方法,要熟悉正切函数的图象,要清楚直线倾斜角的范围.

| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
| A. | 加法 | B. | 减法 | C. | 数量积 | D. | 除法 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1).
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1).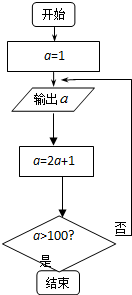 按照如图所示的框图操作,
按照如图所示的框图操作,