题目内容
20.若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|的最大值是( )| A. | 1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$-1 | D. | $\sqrt{2}$ |
分析 由题意可得,$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2}$,故当$\overrightarrow{a}$+$\overrightarrow{b}$与 $\overrightarrow{c}$的方向相反时,|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|取得最大值为$\sqrt{2}$+1.
解答 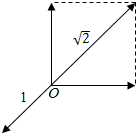 解:若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{2}$,
解:若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{2}$,
故当$\overrightarrow{a}$+$\overrightarrow{b}$与 $\overrightarrow{c}$的方向相反时,|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|取得最大值,
此时,|$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$|=$\sqrt{2}$+1,
故选:B.
点评 本题主要考查两个向量的数量积的运算,求向量的模,属于基础题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | lg7 | B. | lg25 | C. | 1 | D. | lg32 |