题目内容
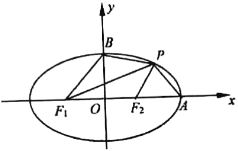
【题目】如图,已知椭圆![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,
,![]() 为椭圆上在第一象限内一点.
为椭圆上在第一象限内一点.
(1)若![]() .
.
①求椭圆的离心率![]() ;
;
②求直线![]() 的斜率.
的斜率.
(2)若![]() ,
,![]() ,
,![]() 成等差数列,且
成等差数列,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)①![]() ; ②
; ②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据![]() 得
得![]() ,即
,即![]() ,可得离心率;②设
,可得离心率;②设![]() 的直线方程,由
的直线方程,由![]() ,得
,得![]() 即可求得斜率;
即可求得斜率;
(2)根据![]() 得离心率的范围
得离心率的范围![]() ,根据
,根据![]() ,
,![]() ,
,![]() 成等差数列,计算化简得
成等差数列,计算化简得![]() ,平方处理成关于离心率
,平方处理成关于离心率![]() 的函数关系,利用函数单调性求范围.
的函数关系,利用函数单调性求范围.
解:(1)①因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
②设![]() 的直线方程为
的直线方程为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,则
,则![]() ,
,
因为![]() 在第一象限,所以
在第一象限,所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)设![]() ,则
,则![]() ,因为
,因为![]() 在第一象限,所以
在第一象限,所以![]() ,
,
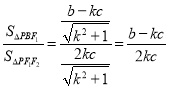 ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,![]() 成等差数列,所以
成等差数列,所以![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,又由已知
,又由已知![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]()
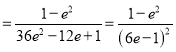 ,
,
令![]() ,所以
,所以![]() ,
,
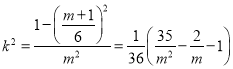
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为![]() 为椭圆上在第一象限内一点,所以
为椭圆上在第一象限内一点,所以![]() ,所以
,所以![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
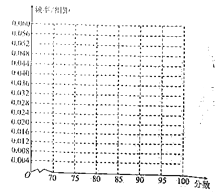
(2)当地环保部门随机抽测了2018年11月的空气质量指数,其数据如下表:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品,花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2018年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 |
|
空气质量指数级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |