题目内容
【题目】如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面ABCD,
面ABCD,![]() ,F为棱
,F为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
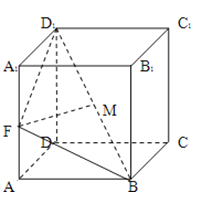
(1)求证:![]() 面ABCD;
面ABCD;
(2)判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析 (2)![]() 平面
平面![]() ,证明见解析 (3)
,证明见解析 (3)![]()
【解析】
(1)连接AC、BD交于点O,再连接OM,利用三角形中位线定理结合平行四边形的性质,得四边形MOAF是平行四边形,从而![]() ,所以
,所以![]() 平面ABCD;
平面ABCD;
(2)![]() 平面
平面![]() ,先证明
,先证明![]() 平面
平面![]() ,再结合
,再结合![]() ,可得
,可得![]() 平面
平面![]() ;
;
(3)过点B作![]() 于H,可证出
于H,可证出![]() 平面
平面![]() ,从而BH是三棱锥
,从而BH是三棱锥![]() 的高,算出
的高,算出![]() 的面积并结合锥体体积公式,可得三棱锥
的面积并结合锥体体积公式,可得三棱锥![]() 的体积.
的体积.
解:(1)接AC、BD交于点O,再连接OM,
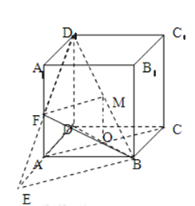
![]() 中,OM是中位线,
中,OM是中位线,![]() 且
且![]() ,
,
∵矩形![]() 中,
中,![]() 且
且![]() ,
,
![]() 且
且![]() ,可得四边形MOAF是平行四边形,
,可得四边形MOAF是平行四边形,
![]() ,
,
![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() 平面ABCD;
平面ABCD;
(2)![]() 平面
平面![]() ,证明如下
,证明如下
在底面菱形ABCD中,![]() ,
,
又![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() ,
,
![]() 是平面
是平面![]() 内的相交直线,
内的相交直线,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(3)过点B作![]() ,垂足为H,
,垂足为H,

![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
![]() ,
,
![]() 是平面
是平面![]() 内的相交直线,
内的相交直线,
![]() 平面
平面![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
因此,三棱锥![]() 的体积
的体积![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目