题目内容
【题目】将编号为1,2,…,18的18名乒乓球运动员分配在9张球台上进行单打比赛,规定每一张球台上两选手编号之和均为大于4的平方数.记{7号与18号比赛}为事件p.则p为( ).
A. 不可能事件 B. 概率为![]() 的随机事件
的随机事件
C. 概率为![]() 的随机事件 D. 必然事件
的随机事件 D. 必然事件
【答案】D
【解析】
由于编号最大的两数之和为![]() ,所以,同一张球台上两选手编号之和只能取3个平方数:25、16、9.现设同一张球台上两选手编号和为25、16、9的分别有x、y、z(x、y、z均为非负整数)个.依题意有
,所以,同一张球台上两选手编号之和只能取3个平方数:25、16、9.现设同一张球台上两选手编号和为25、16、9的分别有x、y、z(x、y、z均为非负整数)个.依题意有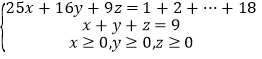 ,即
,即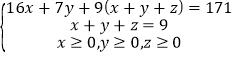 .得
.得![]() .
.
又由![]() ,知x只能取非负整数0,1,2,3,4,5.逐一代入检验,可得方程唯一的非负整数解
,知x只能取非负整数0,1,2,3,4,5.逐一代入检验,可得方程唯一的非负整数解![]() ,
,![]() ,
,![]() .
.
下面讨论9张球台上的选手对阵情况.
(1)由x=3,知平方数为25只能有3个,而编号不小于16的3个选手18,17,16对应的平方数又只能为25,故“两选手编号和为25”的只能是:18与7对阵,17与8对阵,16与9对阵.
(2)由![]() ,知去掉18,17,16,9,8,7后剩下的12个选手对应的平方数能且只能为16,有:1与15对阵,2与14对阵,3与13对阵,4与12对阵,5与11对阵,6与10对阵.
,知去掉18,17,16,9,8,7后剩下的12个选手对应的平方数能且只能为16,有:1与15对阵,2与14对阵,3与13对阵,4与12对阵,5与11对阵,6与10对阵.
所以,规定能够实现,且实现方案是唯一的.9张球台上选手对阵情况为:![]() .
.
事件p为必然事件.选D.

【题目】为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 5 | 25 |
经常使用手机 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则有( )的把握认为经常使用手机对数学学习成绩有影响.
参考公式: ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.97.5%B.99%C.99.5%D.99.9%