题目内容
(本小 题满分12分)
题满分12分)
设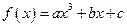
 为奇函数,其图象在点
为奇函数,其图象在点
 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数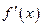 的最小值为
的最小值为
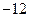 .
. 求
求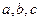 的值
的值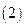 .求函数
.求函数 的单调递增
的单调递增 区间,极大值和极小值,并求函数
区间,极大值和极小值,并求函数 在
在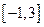 上的最大值与最小值.
上的最大值与最小值.
解:
 为奇函数,
为奇函数,
即

 的最小值为
的最小值为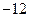 ,zxxk
,zxxk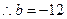
又直线 的斜率为
的斜率为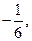
因此 ,
,
故
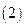
 ,
,
列表如下
所以函数


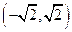
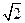

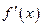
+ 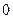
- 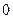
+ 

极大 
极小 
 的单调递增区间为
的单调递增区间为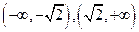
解析

练习册系列答案
相关题目
题目内容
(本小 题满分12分)
题满分12分)
设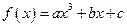
 为奇函数,其图象在点
为奇函数,其图象在点
 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数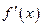 的最小值为
的最小值为
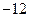 .
. 求
求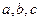 的值
的值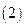 .求函数
.求函数 的单调递增
的单调递增 区间,极大值和极小值,并求函数
区间,极大值和极小值,并求函数 在
在 上的最大值与最小值.
上的最大值与最小值.
解:
 为奇函数,
为奇函数,
即

 的最小值为
的最小值为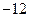 ,zxxk
,zxxk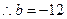
又直线 的斜率为
的斜率为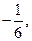
因此 ,
,
故
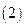
 ,
,
列表如下
所以函数


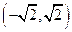
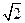

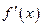
+ 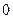
- 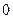
+ 

极大 
极小 
 的单调递增区间为
的单调递增区间为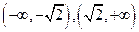
解析
