题目内容
(本小题满分12分)一个盒子中装有大小相同的2个红球和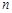 个白球,从中任取2个球.
个白球,从中任取2个球.
(Ⅰ)若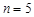 ,求取到的2个球恰好是一个红球和一个白球的概率;
,求取到的2个球恰好是一个红球和一个白球的概率;
(Ⅱ)若取到的2个球中至少有1个红球的概率为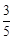 ,求
,求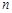 .
.
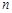 个白球,从中任取2个球.
个白球,从中任取2个球.(Ⅰ)若
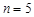 ,求取到的2个球恰好是一个红球和一个白球的概率;
,求取到的2个球恰好是一个红球和一个白球的概率;(Ⅱ)若取到的2个球中至少有1个红球的概率为
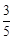 ,求
,求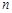 .
.(1)若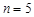 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为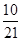 ;
;
(2)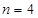 .
.
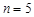 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为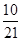 ;
;(2)
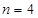 .
.本试题主要是考查了古典概型概率的计算,以及组合数公式的灵活运用,问题,同时对立事件的概念和公式的灵活运用,是解决第二问的关键。
(1)因为一个盒子中装有大小相同的2个红球和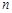 个白球,从中任取2个球.所有情况为
个白球,从中任取2个球.所有情况为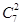
当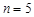 ,求取到的2个球恰好是一个红球和一个白球的情况有
,求取到的2个球恰好是一个红球和一个白球的情况有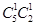 ;结合古典概型概率得到。
;结合古典概型概率得到。
(2)利用对立事件记“取到的2个球中至少有1个红球”为事件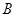 ,
,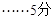
由题意,得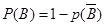 ,即为
,即为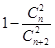 ,这样可以得到关于n的关系式,从而得到求解。
,这样可以得到关于n的关系式,从而得到求解。
解:(Ⅰ)记“取到的2个球恰好是一个红球和一个白球”为事件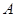 .
.
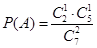
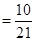
(Ⅱ)记“取到的2个球中至少有1个红球”为事件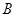 ,
,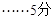
由题意,得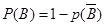
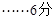
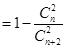
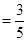
化简得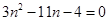 ,
,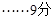
解得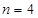 ,或
,或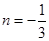 (舍去),
(舍去),
故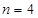 .
.
答:(1)若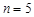 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为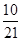 ;
;
(2)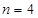 .
.
(1)因为一个盒子中装有大小相同的2个红球和
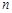 个白球,从中任取2个球.所有情况为
个白球,从中任取2个球.所有情况为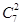
当
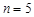 ,求取到的2个球恰好是一个红球和一个白球的情况有
,求取到的2个球恰好是一个红球和一个白球的情况有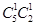 ;结合古典概型概率得到。
;结合古典概型概率得到。(2)利用对立事件记“取到的2个球中至少有1个红球”为事件
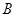 ,
,
由题意,得
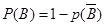 ,即为
,即为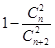 ,这样可以得到关于n的关系式,从而得到求解。
,这样可以得到关于n的关系式,从而得到求解。解:(Ⅰ)记“取到的2个球恰好是一个红球和一个白球”为事件
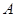 .
.
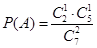
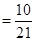
(Ⅱ)记“取到的2个球中至少有1个红球”为事件
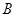 ,
,
由题意,得
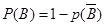
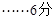
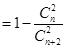
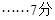
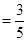
化简得
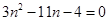 ,
,
解得
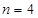 ,或
,或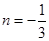 (舍去),
(舍去),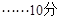
故
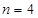 .
.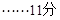
答:(1)若
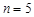 ,取到的2个球恰好是一个红球和一个白球的概率为
,取到的2个球恰好是一个红球和一个白球的概率为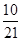 ;
;(2)
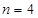 .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
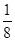
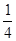
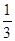
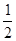
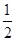
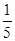
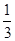
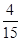
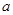 ,乙猜甲刚才想的数字,把乙猜出的数字记为
,乙猜甲刚才想的数字,把乙猜出的数字记为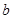 ,且
,且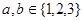 ,若
,若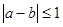 ,则称甲乙“心有灵犀”,则他们“心有灵犀”的概率为( )
,则称甲乙“心有灵犀”,则他们“心有灵犀”的概率为( )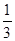
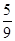
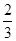
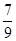
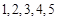 的
的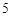 个小球,这些小球除标注的数字外完全相同,现从中随机取出
个小球,这些小球除标注的数字外完全相同,现从中随机取出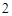 个小球,则取出小球标注的数字之差的绝对值为
个小球,则取出小球标注的数字之差的绝对值为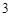 的概率是 .
的概率是 .


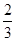
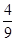
 ,
, ,记
,记 为抛掷一枚骰子出现的点数,则
为抛掷一枚骰子出现的点数,则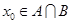 的概率等于 ;
的概率等于 ;