题目内容
17.已知logax=1,logbx=2,logcx=3,则logabcx=$\frac{6}{11}$.分析 根据对数的换底公式进行化简即可得到结论.
解答 解:∵logax=1,logbx=2,logcx=3,
∴logxa=1,logxb=$\frac{1}{2}$,logxc=$\frac{1}{3}$,
∴logxabc=logxa+logxb=logxc=1+$\frac{1}{2}$+$\frac{1}{3}$=$\frac{11}{6}$,
∴logabcx=$\frac{1}{lo{g}_{x}abc}$=$\frac{6}{11}$,
故答案为:$\frac{6}{11}$.
点评 本题主要考查对数的计算,根据对数的换底公式是解决本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
2.已知x=lnπ,y=log5$\sqrt{2}$,$z=e^{-\frac{1}{2}}$,则( )
| A. | y<z<x | B. | z<x<y | C. | z<y<x | D. | x<y<z |
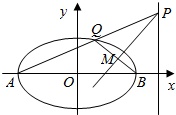 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?