题目内容
5.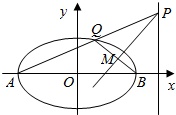 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点为A、B,点P在直线x=t(t为常数)上,线段AP与椭圆C交于点Q(异于点A),设以PQ为直径的圆交直线BQ于点M(异于点Q),问直线PM是否恒过一个定点?
分析 设Q(x0,y0),可表示出AQ的方程,进而表示出P的坐标,由QB⊥PM可求得直线PM的方程,令y=0即可得到直线PM与x轴的交点的横坐标,再根据点Q在椭圆上即可求出x的值,从而得出结论.
解答 解:设Q(x0,y0)(y0≠0),则直线AQ的方程为y=$\frac{{y}_{0}}{{x}_{0}+a}$(x+a),
∴P的坐标为P(t,$\frac{(t+a){y}_{0}}{{x}_{0}+a}$),
又直线QB的斜率=$\frac{{y}_{0}}{{x}_{0}-a}$,而PQ为直径,∴QB⊥PM,
∴直线PM的斜率=-$\frac{{x}_{0}-a}{{y}_{0}}$,
从而直线PM的方程为y-$\frac{(t+a){y}_{0}}{{x}_{0}+a}$=-$\frac{{x}_{0}-a}{{y}_{0}}$(x-t),
令y=0,得直线PM与x轴的交点的横坐标为x=t+$\frac{(t+a){{y}_{0}}^{2}}{{{x}_{0}}^{2}-{a}^{2}}$
又点Q在椭圆上,∴$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1$,
∴x=$\frac{{c}^{2}t-a{b}^{2}}{{a}^{2}}$,
∴直线PM与x轴的交点为定点,且该定点的坐标为($\frac{{c}^{2}t-a{b}^{2}}{{a}^{2}}$,0).
点评 本题考查直线与圆锥曲线的位置关系、椭圆方程的求解及直线方程的求法,考查学生综合运用所学知识分析解决问题的能力,结合性强,有一定难度.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
15.(文)设全集U=R,集合A={x|x2+4x<0},集合B={x|x<-2},则图中阴影部分表示的集合为( )
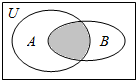

| A. | {x|-4<x<-2} | B. | {x|-4<x<0} | C. | {x|x>0} | D. | {x|x<-2} |
15.对于?x1$∈(0,\frac{1}{2}]$,?x2$∈(0,\frac{1}{2}]$,4${\;}^{{x}_{1}}$<logax2恒成立,则a取值范围是( )
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | (0,$\frac{\sqrt{2}}{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
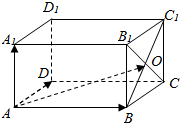 如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.