题目内容
8．若函数y=log2[ax2+（a-1）x+$\frac{1}{4}$]的定义域为R，求实数a的取值范围．若值域为R呢？分析 依题意，令g（x）=x2+（k+2）x+$\frac{5}{4}$，利用g（x）＞0恒成立即可求得定义域为R时，实数a的取值范围，
再令（0，+∞）⊆g（x）的值域．可得值域为R时，实数a的取值范围．
解答 解：∵函数y=log2[ax2+（a-1）x+$\frac{1}{4}$]的定义域为R，
令g（x）=ax2+（a-1）x+$\frac{1}{4}$，
则g（x）＞0恒成立，
∴$\left\{\begin{array}{l}a＞0\\△={（a-1）}^{2}-a＜0\end{array}\right.$
解得a∈（$\frac{3-\sqrt{5}}{2}$，$\frac{3+\sqrt{5}}{2}$），
若函数y=log2[ax2+（a-1）x+$\frac{1}{4}$]的值域为R，
则（0，+∞）⊆g（x）的值域．
∴$\left\{\begin{array}{l}a＞0\\△={（a-1）}^{2}-a≥0\end{array}\right.$，或a=0
解得a∈[0，$\frac{3-\sqrt{5}}{2}$]∪[$\frac{3+\sqrt{5}}{2}$，+∞），
点评 本题考查函数恒成立问题，着重考查对数函数的定义域，考查△的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
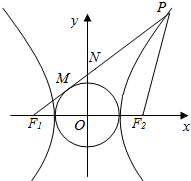已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，P为双曲线右支上一点，直线PF1与圆x2+y2=a2相切，且|PF2|=|F1F2|，则该双曲线的离心率e是$\frac{5}{3}$．