题目内容
2.已知x=lnπ,y=log5$\sqrt{2}$,$z=e^{-\frac{1}{2}}$,则( )| A. | y<z<x | B. | z<x<y | C. | z<y<x | D. | x<y<z |
分析 利用对数函数和指数函数的单调性能比较x=lnπ,y=log5$\sqrt{2}$,$z=e^{-\frac{1}{2}}$的大小.
解答 解:∵x=lnπ>lne=1,
y=log5$\sqrt{2}$<$lo{g}_{5}\sqrt{5}$=$\frac{1}{2}$,
$z=e^{-\frac{1}{2}}$=$\frac{1}{\sqrt{e}}$>$\frac{1}{\sqrt{4}}$=$\frac{1}{2}$,且$\frac{1}{\sqrt{e}}$<1,
∴y<z<x.
故选:A.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数和指数函数的单调性的合理运用.

练习册系列答案
相关题目
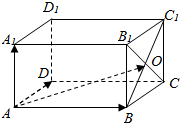 如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.
如图,在平行六面体ABCD-A1B1C1D1中,B1C∩BC1=O,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=2.