题目内容
等差数列{an}的前n项和为Sn,a1=1+
,S3=9+3
.
(1)求数列{an}的通项an与前n项和为Sn;
(2)设bn=
(n∈N+),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
| 2 |
| 2 |
(1)求数列{an}的通项an与前n项和为Sn;
(2)设bn=
| Sn |
| n |
(1)由已知得
,∴d=2,
故an=2n-1+
,Sn=n(n+
).
(2)由(Ⅰ)得bn=
=n+
.
假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则bq2=bpbr.
即(q+
)2=(p+
)(r+
).
∴(q2-pr)+(2q-p-r)
=0,
∵p,q,r∈N*,
∴
,
∴(
)2=pr,(p-r)2=0,
∴p=r.
与p≠r矛盾.
所以数列{bn}中任意不同的三项都不可能成等比数列.
|
故an=2n-1+
| 2 |
| 2 |
(2)由(Ⅰ)得bn=
| Sn |
| n |
| 2 |
假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则bq2=bpbr.
即(q+
| 2 |
| 2 |
| 2 |
∴(q2-pr)+(2q-p-r)
| 2 |
∵p,q,r∈N*,
∴
|
∴(
| p+r |
| 2 |
∴p=r.
与p≠r矛盾.
所以数列{bn}中任意不同的三项都不可能成等比数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
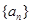 的前
的前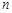 项和为
项和为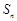 ,且
,且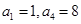 ,则
,则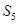 = .
= .