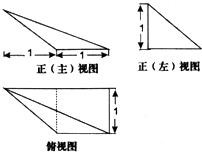
题目内容
5.已知向量$\overrightarrow{a}$=(cosx,-$\frac{1}{2}$),$\overrightarrow{b}$=($\sqrt{3}$sin x,cos 2x),x∈R,设函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(Ⅰ)求f(x)在[0,$\frac{π}{2}$]上的最大值和最小值.
(Ⅱ)求 f(x)的单调增区间.
分析 (I)利用数量积运算性质可得函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}sinxcosx$$-\frac{1}{2}$cos2x=$sin(2x-\frac{π}{6})$.
由x∈[0,$\frac{π}{2}$],可得$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$,$sin(2x-\frac{π}{6})$∈$[-\frac{1}{2},1]$.即可得出f(x)在[0,$\frac{π}{2}$]上的最大值和最小值.
(II)由$-\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{π}{2}+2kπ$,解得即可得出f(x)的单调增区间.
解答 解:(I)函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=$\sqrt{3}sinxcosx$$-\frac{1}{2}$cos2x=$\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x$=$sin(2x-\frac{π}{6})$.
∵x∈[0,$\frac{π}{2}$],∴$-\frac{π}{6}≤2x-\frac{π}{6}≤\frac{5π}{6}$,
∴$sin(2x-\frac{π}{6})$∈$[-\frac{1}{2},1]$.
∴f(x)在[0,$\frac{π}{2}$]上的最大值和最小值分别为1,$-\frac{1}{2}$.
(II)由$-\frac{π}{2}+2kπ≤2x-\frac{π}{6}≤\frac{π}{2}+2kπ$,解得$kπ-\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$(k∈Z).
∴f(x)的单调增区间为$[kπ-\frac{π}{6},kπ+\frac{π}{3}]$(k∈Z).
点评 本题考查了向量数量积的关系、三角函数的单调性与最值,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
| A. | 平行 | B. | 重合 | C. | 垂直 | D. | 以上都不是 |
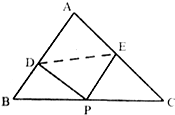 已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).
已知△ABC中,角A,B,C所对的边分别为a,b,c,若sin2 A+sin2 B=sin2C+sin AsinB,ccosB=b(1-cosC).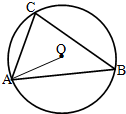 如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.