题目内容
甲、乙两地相距S千米,汽车从甲地匀速驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的平方成正比,比例系数为b,固定部分为a元
(1)把全程运输成本y(元)表示为v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?

(1)把全程运输成本y(元)表示为v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(1)函数及其定义域为y=S( +bv),v∈(0,c
+bv),v∈(0,c . (2) 为使全程运输成本y最小,当
. (2) 为使全程运输成本y最小,当 ≤c时,行驶速度应为v=
≤c时,行驶速度应为v= , 当
, 当 >c时行驶速度应为v=c.
>c时行驶速度应为v=c.
 +bv),v∈(0,c
+bv),v∈(0,c . (2) 为使全程运输成本y最小,当
. (2) 为使全程运输成本y最小,当 ≤c时,行驶速度应为v=
≤c时,行驶速度应为v= , 当
, 当 >c时行驶速度应为v=c.
>c时行驶速度应为v=c.(1)依题意知,汽车从甲地匀速行驶到乙地所用时间为 ,全程运输成本为y=a·
,全程运输成本为y=a· +bv2·
+bv2· =S(
=S( +bv)
+bv)
∴所求函数及其定义域为y=S( +bv),v∈(0,c
+bv),v∈(0,c .
.
(2)依题意知,S、a、b、v均为正数
∴S( +bv)≥2S
+bv)≥2S ①
①
当且仅当 =bv,即v=
=bv,即v= 时,①式中等号成立
时,①式中等号成立


若 ≤c则当v=
≤c则当v= 时,有ymin=2S
时,有ymin=2S ;
;
若 >c,则当v∈(0,c
>c,则当v∈(0,c 时,有S(
时,有S( +bv)-S(
+bv)-S( +bc)
+bc)
=S[( -
- )+(bv-bc)]=
)+(bv-bc)]= (c-v)(a-bcv)
(c-v)(a-bcv)
∵c-v≥0,且c>bc2, ∴a-bcv≥a-bc2>0
∴S( +bv)≥S(
+bv)≥S( +bc),当且仅当v=c时等号成立,
+bc),当且仅当v=c时等号成立,
也即当v=c时,有ymin=S( +bc);
+bc);
综上可知,为使全程运输成本y最小,当 ≤c时,行驶速度应为v=
≤c时,行驶速度应为v= , 当
, 当 >c时行驶速度应为v=c.
>c时行驶速度应为v=c.
解法二: (1)同解法一.
(2)∵函数y=S( +bv), v∈(0,+∞),
+bv), v∈(0,+∞),
当x∈(0, )时,y单调减小,
)时,y单调减小,
当x∈( ,+∞)时y单调增加,
,+∞)时y单调增加,
当x= 时y取得最小值,而全程运输成本函数为y=Sb(v+
时y取得最小值,而全程运输成本函数为y=Sb(v+ ),v∈(0,c
),v∈(0,c :
:


∴当 ≤c时,则当v=
≤c时,则当v= 时,y最小,若
时,y最小,若 >c时,则当v=c时,y最小. 结论同上.
>c时,则当v=c时,y最小. 结论同上.
 ,全程运输成本为y=a·
,全程运输成本为y=a· +bv2·
+bv2· =S(
=S( +bv)
+bv)∴所求函数及其定义域为y=S(
 +bv),v∈(0,c
+bv),v∈(0,c .
.(2)依题意知,S、a、b、v均为正数
∴S(
 +bv)≥2S
+bv)≥2S ①
①当且仅当
 =bv,即v=
=bv,即v= 时,①式中等号成立
时,①式中等号成立


若
 ≤c则当v=
≤c则当v= 时,有ymin=2S
时,有ymin=2S ;
;若
 >c,则当v∈(0,c
>c,则当v∈(0,c 时,有S(
时,有S( +bv)-S(
+bv)-S( +bc)
+bc)=S[(
 -
- )+(bv-bc)]=
)+(bv-bc)]= (c-v)(a-bcv)
(c-v)(a-bcv)∵c-v≥0,且c>bc2, ∴a-bcv≥a-bc2>0
∴S(
 +bv)≥S(
+bv)≥S( +bc),当且仅当v=c时等号成立,
+bc),当且仅当v=c时等号成立,也即当v=c时,有ymin=S(
 +bc);
+bc);综上可知,为使全程运输成本y最小,当
 ≤c时,行驶速度应为v=
≤c时,行驶速度应为v= , 当
, 当 >c时行驶速度应为v=c.
>c时行驶速度应为v=c.解法二: (1)同解法一.
(2)∵函数y=S(
 +bv), v∈(0,+∞),
+bv), v∈(0,+∞),当x∈(0,
 )时,y单调减小,
)时,y单调减小,当x∈(
 ,+∞)时y单调增加,
,+∞)时y单调增加,当x=
 时y取得最小值,而全程运输成本函数为y=Sb(v+
时y取得最小值,而全程运输成本函数为y=Sb(v+ ),v∈(0,c
),v∈(0,c :
:

∴当
 ≤c时,则当v=
≤c时,则当v= 时,y最小,若
时,y最小,若 >c时,则当v=c时,y最小. 结论同上.
>c时,则当v=c时,y最小. 结论同上. 
练习册系列答案
相关题目
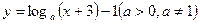 的图像恒过点A,若点A在直线
的图像恒过点A,若点A在直线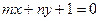 上,其中
上,其中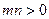 ,则
,则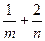 的最小值为 .
的最小值为 .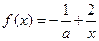 ,若
,若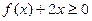 在(0,+
在(0,+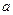 )上恒成立,求
)上恒成立,求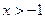 ,则
,则 =_____时,
=_____时,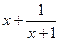 有最小值,最小值为_____.
有最小值,最小值为_____. 对任意正实数
对任意正实数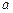 、
、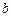 都成立,则
都成立,则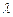 的最大值是( )
的最大值是( )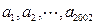 均为正实数,且
均为正实数,且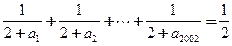 ,则
,则 的最小值为____________________.
的最小值为____________________.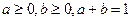 ,则
,则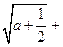
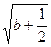 的范围是____________
的范围是____________