题目内容
解关于x的不等式|2x+m|<x-m(x∈R).
本题考查含有绝对值不等式的解法.解题关键是对m进行分类讨论.
本题考查含有绝对值不等式的解法.解题关键是对m进行分类讨论.
当m<0时,-2m>0,此时原不等式的解集为{x|0<x<-2m};
当m≥0时,-2m≤0,原不等式的解集为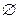 .
.
当m≥0时,-2m≤0,原不等式的解集为
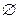 .
.∵|2x+m|<x-m,
∴m-x<2x+m<x-m.
∴0<x<-2m.
∴当m<0时,-2m>0,此时原不等式的解集为{x|0<x<-2m};
当m≥0时,-2m≤0,原不等式的解集为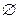 .
.
∴m-x<2x+m<x-m.
∴0<x<-2m.
∴当m<0时,-2m>0,此时原不等式的解集为{x|0<x<-2m};
当m≥0时,-2m≤0,原不等式的解集为
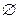 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
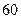 米,宽
米,宽 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当 +
+ =1,求x+y的最小值;
=1,求x+y的最小值; ,求函数y=4x-2+
,求函数y=4x-2+ 的最大值;
的最大值;
 则
则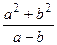 的最小值是( ).
的最小值是( ).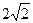 B
B 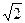 C 2 D 1
C 2 D 1 对任意的
对任意的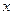 、
、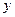 恒成立,则正实数
恒成立,则正实数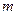 的最小值为
的最小值为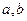 满足
满足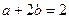 ,则
,则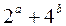 的最小值为__________.
的最小值为__________.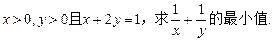
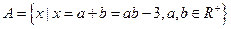 ,全集
,全集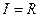 ,则
,则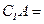 ___________
___________