题目内容
已知函数f(x)= sin2x+sin xcos x,x∈
sin2x+sin xcos x,x∈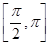 .
.
(1)求f(x) 的零点;
(2)求f(x)的最大值和最小值.
 sin2x+sin xcos x,x∈
sin2x+sin xcos x,x∈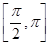 .
.(1)求f(x) 的零点;
(2)求f(x)的最大值和最小值.
(1) 或π.(2)最大值为
或π.(2)最大值为 ,最小值为-1+
,最小值为-1+ .
.
 或π.(2)最大值为
或π.(2)最大值为 ,最小值为-1+
,最小值为-1+ .
.(1)令f(x)=0得sin x·( sin x+cos x)=0,所以sin x=0,或tan x=-
sin x+cos x)=0,所以sin x=0,或tan x=- .
.
由sin x=0,x∈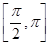 ,得x=π;由tan x=-
,得x=π;由tan x=- ,x∈
,x∈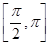 ,得x=
,得x= .
.
综上,函数f(x)在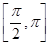 上的零点为
上的零点为 或π.
或π.
(2)f(x)= (1-cos 2x)+
(1-cos 2x)+ sin 2x=sin
sin 2x=sin +
+ .
.
因为x∈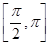 ,所以2x-
,所以2x- ∈
∈ .
.
当2x- =
= ,即x=
,即x= 时,f(x)的最大值为
时,f(x)的最大值为 ;
;
当2x- =
= ,即x=
,即x= 时,f(x)的最小值为-1+
时,f(x)的最小值为-1+ .
.
 sin x+cos x)=0,所以sin x=0,或tan x=-
sin x+cos x)=0,所以sin x=0,或tan x=- .
.由sin x=0,x∈
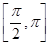 ,得x=π;由tan x=-
,得x=π;由tan x=- ,x∈
,x∈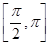 ,得x=
,得x= .
.综上,函数f(x)在
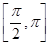 上的零点为
上的零点为 或π.
或π.(2)f(x)=
 (1-cos 2x)+
(1-cos 2x)+ sin 2x=sin
sin 2x=sin +
+ .
.因为x∈
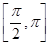 ,所以2x-
,所以2x- ∈
∈ .
.当2x-
 =
= ,即x=
,即x= 时,f(x)的最大值为
时,f(x)的最大值为 ;
;当2x-
 =
= ,即x=
,即x= 时,f(x)的最小值为-1+
时,f(x)的最小值为-1+ .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象如图所示,则f(0)=________.
的图象如图所示,则f(0)=________.
 的图像与
的图像与 的图像的两个相邻交点间的距离为
的图像的两个相邻交点间的距离为 ,要得到
,要得到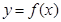 的图像,只须把
的图像,只须把 的图像 ( )
的图像 ( ) 个单位
个单位 个单位
个单位 的最小正周期为
的最小正周期为 .
. 的定义域;
的定义域; ,
, ,
, ,
, .那么下面命题中真命题的序号是( )
.那么下面命题中真命题的序号是( ) 的最大值为
的最大值为 ②
② 在
在 上是增函数 ④
上是增函数 ④ 上是增函数
上是增函数 在
在 上单调递减,则ω的取值范围是( ).
上单调递减,则ω的取值范围是( ).


 ),y=f(x)的部分图象如图所示,则f
),y=f(x)的部分图象如图所示,则f =________.
=________.
 则
则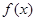 在区间[0,
在区间[0, ]上的最大值与最小值分别是( )
]上的最大值与最小值分别是( )